LeetCode题库
LeetCode 题库
🌍 当前题库题目数:

WANTED 📜
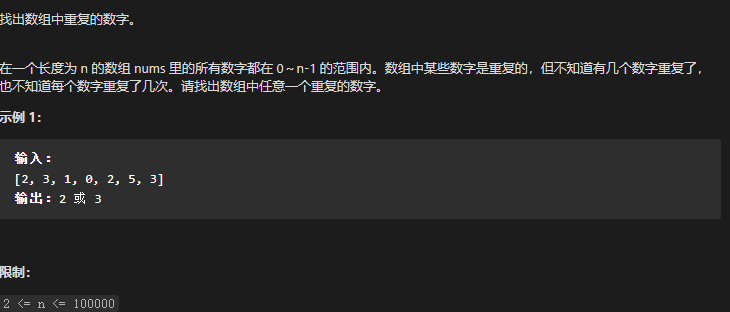
JZ-03. 两数相加 ⭐
思考:
未排序、有重复数字、找出的是任意的重复数字、所有数字大小都在0---n-1的范围内、输出的是重复的那个数字
1. 基于哈希表
Map map = new HashMap();
int i = 0;
while(i<nums.length){
if((int)map.getOrDefault(nums[i],-1) != -1){
return nums[i];
}
map.put(nums[i], nums[i]);
i++;
}
return -1;

时间复杂度 O(N) 空间复杂度 O(N)
2. 原地置换nb
这里确实 应该多看题目给的数字范围在0--n-1思考,这是解这道题的关键,之前的哈希表是没有用到这个条件的
int temp;
for(int i =0; i<nums.length; i++){
while(nums[i] != i){
if(nums[i] == nums[nums[i]]){
return nums[i];
}
temp = nums[nums[i]];
nums[nums[i]] = nums[i];
nums[i] = temp;
}
}
return -1;
理解这里的思想主要是自己想一个数组一步步去进行 有点桶排序的感觉?

这里最后发现问题的关键是 n-1范围内, 索引为i对应的位置上肯定是 i ,然后去判断时 发现重复的元素,肯定是在他的值对应的索引上去找的,如果有这个值,则找到了,没有,则说明还未填上,则填上。
这里主要是还是要掌握桶排序的思想,先去思考能不能通过ON的方式解决问题
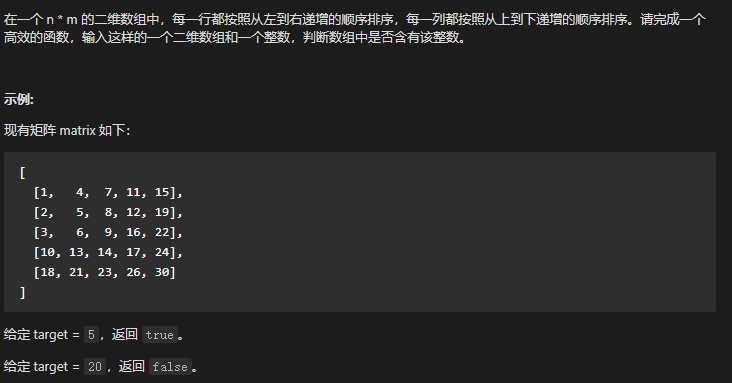
JZ-04. 二维数组中的查找 ⭐⭐
观察:
每行递增、每列递增
1. 自己想的矩阵分割法
2. 翻转矩阵 / 线性搜索
矩阵的右上角开始
int j = matrix[0].length-1;
int i = 0;
int num = 16;
while(true){
if(i<0||j<0) break;
if(matrix[i][j]>num) j--;
else if(matrix[i][j]<num) i++;
else if(matrix[i][j] == num)
System.out.println(num);
JZ-07. 重建二叉树 ⭐⭐
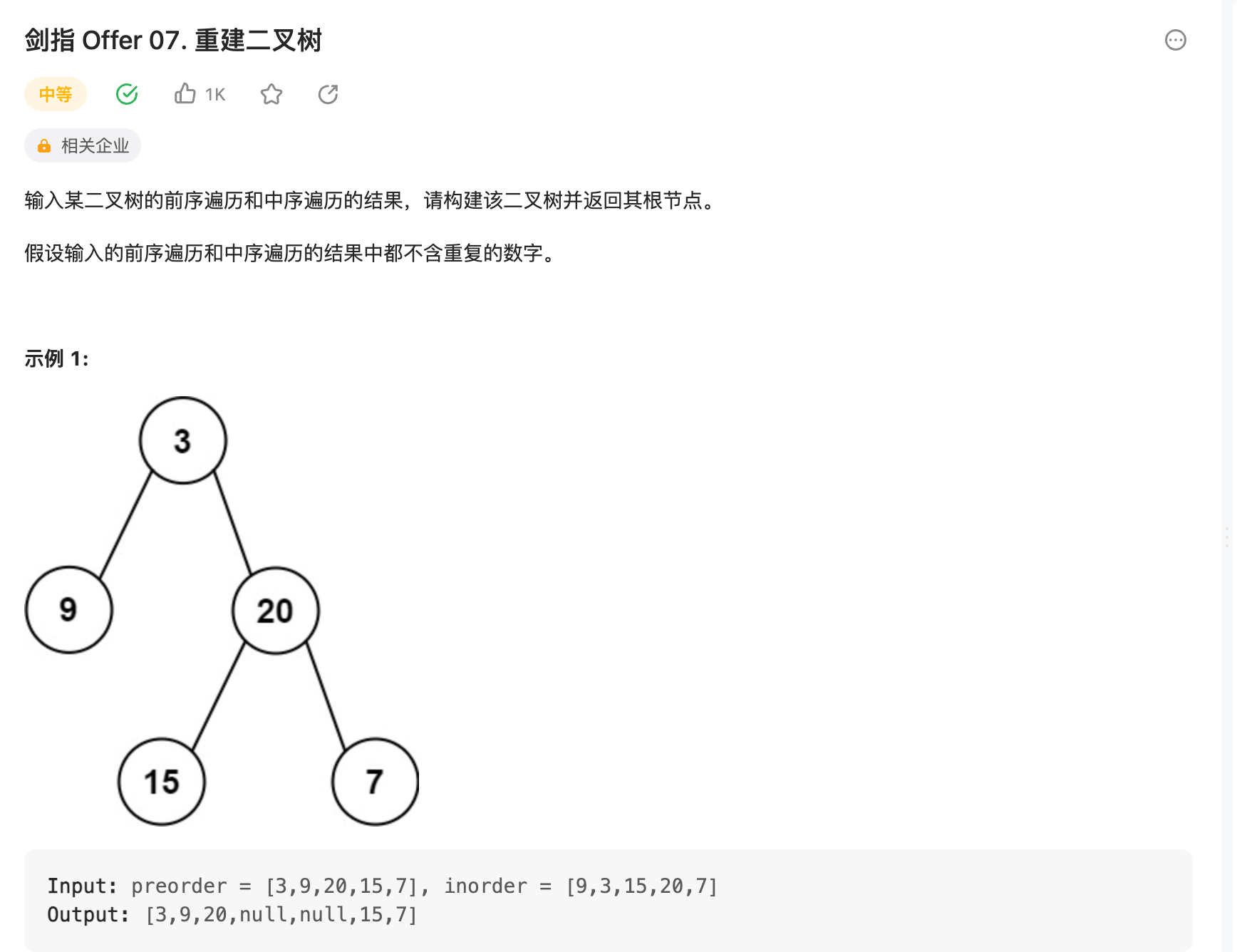
1. 递归
前提理论: 对于任何一棵树而言,前序遍历形式为:
中序遍历形式为
所以思路大概可以确定:
- 通过前序遍历找到根节点
- 通过根节点在中序遍历中确定其左右子树
- 对子树进行同样的操作,但需要注意的是,在子树的划分过程中,要考虑 界限 的问题
- 如果是左子树则左边界与父节点保持一致,修改右边界为父节点的前一个位置
- 如果是右子树则右边界与父节点保持一致,修改坐边界为父节点的后一个位置
可以理解为:构建过程在前序遍历中顺序推动,在中序遍历中动态查找并确定子树范围
class Solution {
static int preIdx = 0;
static Map<Integer, Integer> inMap;
public TreeNode buildTree(int[] preorder, int[] inorder) {
inMap= new HashMap<>();
for(int i = 0; i < preorder.length; i++) {
inMap.put(inorder[i], i);
}
preIdx = 0;
return build(preorder, inorder, 0, preorder.length - 1);
}
public TreeNode build(int[] preorder, int[] inorder, int l, int r) {
// notice the problem of bound overflow
if(preIdx >= inorder.length || r < l ) {
return null;
}
if(r - l == 0) {
// Don't forget to increment `preIdx`
preIdx++;
return new TreeNode(inorder[l]);
}
// Optimize: use map to reduce each foreach below
int inIdx = inMap.get(preorder[preIdx++]);
TreeNode node = new TreeNode(inorder[inIdx]);
// the key to show recursion
node.left = build(preorder, inorder, l, inIdx - 1);
node.right = build(preorder, inorder, inIdx + 1, r);;
return node;
}
}
JZ-10. 青蛙跳台阶 ⭐
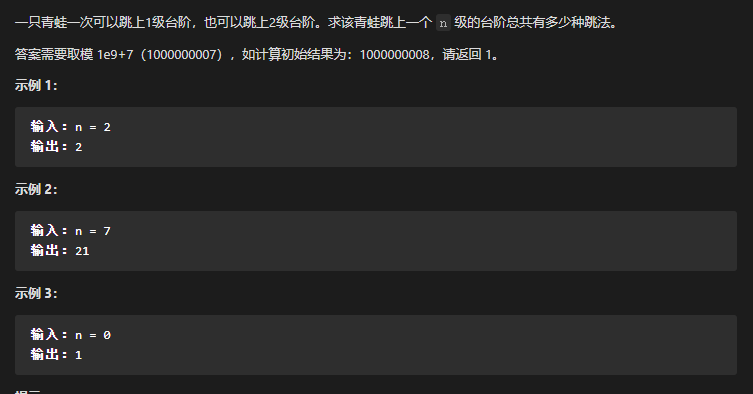
思考
就是拼砖头的递归思想
返回格式 ()+1
1. 递归(超时)
if(num == 0 || num == 1){
return 1;
}
if(num == 2){
return 2;
}
return getMax(num-2)+getMax(num - 1) ;
递归的时间复杂度是On*n 空间复杂度 On 所以肯定超时了
2. 动态规划
典型的斐波那契数列问题,艹,就是一个三个缓存数进行斐波那契数列的运算
为什么是斐波那契?
以后看算法题的时候,先看其通项结构
f(n) = f(n-1) + f(n-2)
int a = 1;
int b = 1;
int sum = 0;
for(int i =0;i< num;i++){
sum = (a+b)%1000000007;
a = b;
b = sum;
}
return a;
时间复杂度 On 空间复杂度 O1
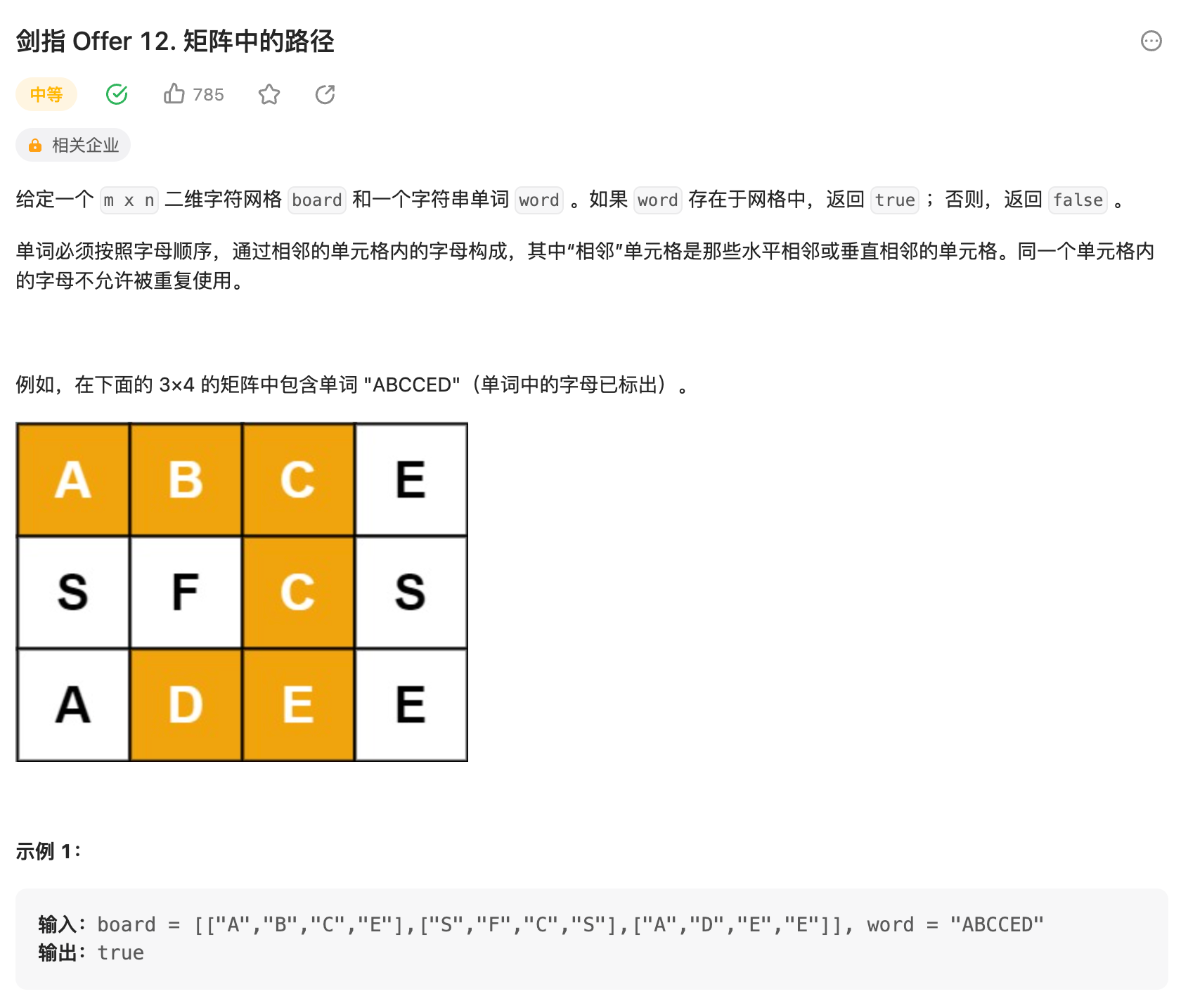
JZ-12. 矩阵中的路径
1. 回溯 DFS
思路,
- 开辟同纬度标志位数组
- 如果当前元素满足条件,则设置标志数组表明该位置的元素已被访问,同时进行以下操作
- 对该元素周围(上下左右)对字符进行下一个word字符的检索。
- 如果都不符合条件,则表明在该元素不符合条件,含有该位置的元素无法构成最终的word单词。将元素上的标志位还原(以便其他位置的元素进行判断)
- 如果当前元素不满足条件,则返回false
class Solution {
public boolean exist(char[][] board, String word) {
int[][] flags = new int[board.length][board[0].length];
// puffed code, need optimize
boolean res = false;
for(int i = 0; i < board.length; i++) {
for(int j = 0; j < board[0].length; j++) {
// optimize, no need for foreach if res is true
if(res) {
return true;
}
// mutiple check to cover all conditions
if(board[i][j] == word.charAt(0)) {
res = dfsFindCurChar(board, flags, word, i, j, 0);
}
}
}
return res;
}
public boolean dfsFindCurChar(char[][] board,int[][] flags, String word, int i, int j, int index) {
if(index == word.length()) {
return true;
}
// avoid bound overflow
if(i < 0 || i >= board.length || j < 0 || j >= board[0].length) {
return false;
}
// if flag is already dropped in at
if(flags[i][j] == 1) {
return false;
}
if(board[i][j] == word.charAt(index)) {
flags[i][j] = 1;
// can be optimzed
boolean onRight = dfsFindCurChar(board, flags, word, i+1, j, index+1);
boolean onLeft = dfsFindCurChar(board, flags, word, i-1, j, index+1);
boolean onDown = dfsFindCurChar(board, flags, word, i, j+1, index+1);
boolean onUp = dfsFindCurChar(board, flags, word, i, j-1, index+1);
// need optimze
if(onRight || onLeft || onDown || onUp) {
return true;
}
}
// if not equate to the char, we need to reset this flag to ensure another incursion could work.
flags[i][j] = 0;
return false;
}
}
优化
一个小的优化例子,比较有趣,不用设置额外的标志位来进行,仅需要把board字符数组中的元素设置为指定字符表明该字符已被访问过即可,并且在失败时进行还原(通过word)即可。
class Solution {
public boolean exist(char[][] board, String word) {
for(int i = 0; i < board.length; i++) {
for(int j = 0; j < board[0].length; j++) {
// code optimization
if(dfsFindCurChar(board, word, i, j, 0)) return true;
}
}
return false;
}
public boolean dfsFindCurChar(char[][] board, String word, int i, int j, int index) {
if(index == word.length()) {
return true;
}
// avoid bound overflow
if(i < 0 || i >= board.length || j < 0 || j >= board[0].length) {
return false;
}
// if flag is already dropped in at
if(board[i][j] == '\0') {
return false;
}
if(board[i][j] == word.charAt(index)) {
board[i][j] = '\0';
// can be optimzed
boolean onRight = dfsFindCurChar(board, word, i+1, j, index+1);
boolean onLeft = dfsFindCurChar(board, word, i-1, j, index+1);
boolean onDown = dfsFindCurChar(board, word, i, j+1, index+1);
boolean onUp = dfsFindCurChar(board, word, i, j-1, index+1);
// need optimze
if(onRight || onLeft || onDown || onUp) {
return true;
}
// vital: if not equate to the char, we need to reset this flag to ensure another incursion could work.
board[i][j] = word.charAt(index);
}
return false;
}
}
剪枝: 同时这里也是基于DFS,所以可以进行剪枝优化,即通过 || 运算符,拿到一个true值就返回结果。
错误总结
慎用自增表达式 i++
在进行回溯的时候老是爱犯一个错误,就是错用自增表达式,这样的情况在之前while循环中也出现过,但场景不同,比较以下代码的不同
boolean onRight = dfsFindCurChar(board, word, i++, j, index++);
boolean onLeft = dfsFindCurChar(board, word, i--, j, index++);
// separator
boolean onRight = dfsFindCurChar(board, word, i+1, j, index+1);
boolean onLeft = dfsFindCurChar(board, word, i-1, j, index+1);
很明显,前者会出现错误,因为i++后的i不再是原来的值,因此i--也会得到错误的值,所以这里涉及原值传递时,慎用自增表达式
JZ-14 -I 剪绳子 ⭐⭐
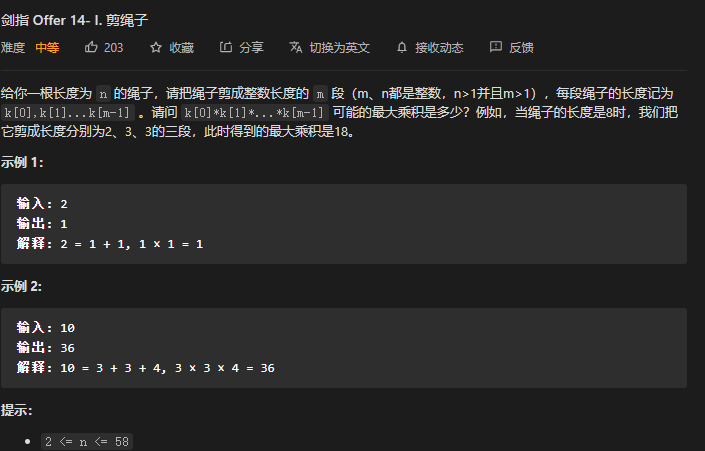
思考:
动态规划、通项式、贪心算法?
后来发现在求On的时候有复杂的情况,就放弃了,应该是数学方面的问题,不应该暴力迭代
O (1):


class Solution {
public int cuttingRope(int n) {
if(n <= 3) return n - 1;
int a = n / 3, b = n % 3;
if(b == 0) return (int)Math.pow(3, a);
if(b == 1) return (int)Math.pow(3, a - 1) * 4;
return (int)Math.pow(3, a) * 2;
}
}
// 作者:jyd
// 链接:https://leetcode-cn.com/problems/jian-sheng-zi-lcof/solution/mian-shi-ti-14-i-jian-sheng-zi-tan-xin-si-xiang-by/
JZ-22. 链表中倒数第k个节点 ⭐
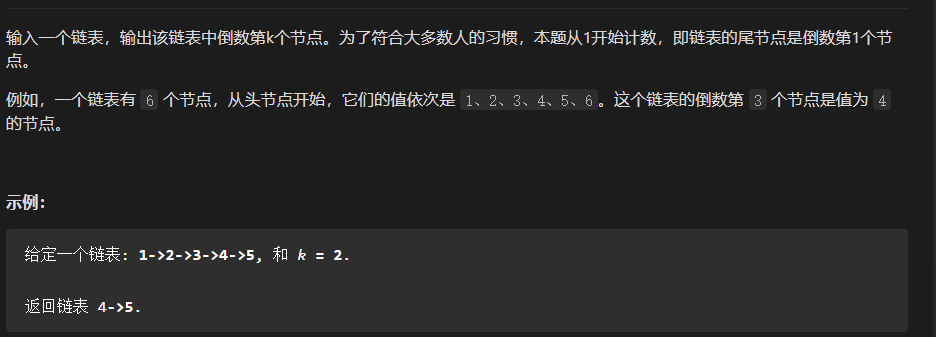
思考
正常情况下,O n+n?
1. 递归寻找?
我最开始准备是 getNode(node.next)先往下去找,找到next为null时再向上返回,但是这时候如何去减k值我就不知道了
这个最后在第三点中得到解决👍
2. 妙妙双指针
让前指针先走k步,然后后指针跟随者前指针一起走
核心的点是在当pre为null时,也就是走到头了,这时候former与pre差k步,也就是倒数第k个元素。
ListNode premer = head;
ListNode former = head;
for(int i =0;i<k;i++){
premer = premer.next;
}
while(premer != null){
premer = premer.next;
former = former.next;
}
return former;

时间复杂度O n 空间复杂度 O2
如果这种问题递归不行的话,就想想双指针会怎么做吧
3. 回溯
📆 2022.10.30 回顾想的解法,主要是解决两个问题
- 回溯时倒数第k个 如何判断,如何判断当前是倒数第几个元素
- 回溯时如何既有当前元素的逆序数,又有当前元素的指针?
class Solution {
public ListNode getKthFromEnd(ListNode head, int k) {
return (ListNode)(method(head, k)[1]);
}
// Object[0] 当前结点的逆序数(m == k 时返回的是结点的data值)
// Object[1] 当前元素:只有逆序数与k相等时才不为空
public Object[] method(ListNode head, int k) {
if(head == null)
return new Object[]{0, null};
Object[] object = method(head.next, k);
int m = (int)object[0] + 1;
if(m == k) {
return new Object[]{head.val, head};
}
if(object[1] != null) {
return object;
}
return new Object[]{m, null};
}
}
这里需要注意的是,回溯时并不是只有mk后就不回溯了,而是之后一直到头结点都有回溯到过程,所以在这个过程中要灵活处理返回到Object[] 确保它就为mk时的那个值
递归?
JZ-24. 反转链表 ⭐
思考
似乎没什么,注意 null
1. 自己写的 pre 指针代码
if(head == null){
return null;
}
if(head.next ==null){
return head;
}
int i = 0;
ListNode prer;
ListNode pre;
ListNode Lastpre;
while(true) {
pre = head;
Lastpre = head;
try{
pre = pre.next;
}catch(NullPointerException e){
pre = null;
}
for (int j = 0; j < i; j++) {
pre = pre.next;
Lastpre = Lastpre.next;
}
prer = pre.next;
Lastpre.next = prer;
pre.next = head;
head = pre;
i++;
if(prer == null){
break;
}
}
return head;
写了很久,结果太拉了,自己都不想分析了

2. 双指针
ListNode cur =null;
ListNode pre = head;
ListNode t ;
while(pre != null){
t = pre.next;
pre.next = cur;
cur = pre; // ①标记
pre = t;
}
return cur;
这里主要还是自己以前的老问题,就是标记1处,这里就理解为是单纯的赋值就行了
3. 递归
if (head == null || head.next == null) {
return head;
}
ListNode ret = reverseList(head.next);
head.next.next = head;
// 5.next = head;
head.next = null;
//此处置空的时候一定要注意关注点是ret 而不是head...
return ret;
递归理解起来有一定的难度
特别是注意ret 和 head的包含关系, 如果理解不了的时候就报head.next.next 用另一个遍历替换 head.next = ret 集中关注在ret上,因为递归,所以内存消耗肯定很多啦
这种递归给我的启示是以后分不清next的时候或者等价关系,就用中间变量去解耦,或者用已知指针替换,这样会更好理解一些
Jz-47. 礼物的最大价值 ⭐⭐
1. 递归
2. 动态规划
public static int getMax(int[][] matrix){
for( int i =0;i< matrix.length ; i++){
for(int j = 0;j<matrix[0].length;j++){
if(i == 0&& j ==0 ) continue;
if(i == 0){
matrix[i][j] += matrix[i][j-1];
}
else if(j == 0){
matrix[i][j] += matrix[i-1][j];
}
else {
matrix[i][j] += Math.max(matrix[i][j-1],matrix[i-1][j]);
}
}
}
return matrix[matrix.length-1][matrix[0].length-1];
}
}
时间复杂度 O m*n 空间复杂度 O 1
回顾动态规划的思想,这种问题还是很典型,这种动态规划的思想会破坏原有矩阵
继续优化
对矩阵很大的情况,很少有可能会在第一行或者第一列进行加,所以这个时候可以先进行初始化。然后相当于从[1] [1]开始
int m = grid.length, n = grid[0].length;
for(int j = 1; j < n; j++) // 初始化第一行
grid[0][j] += grid[0][j - 1];
for(int i = 1; i < m; i++) // 初始化第一列
grid[i][0] += grid[i - 1][0];
for(int i = 1; i < m; i++)
for(int j = 1; j < n; j++)
grid[i][j] += Math.max(grid[i][j - 1], grid[i - 1][j]);
return grid[m - 1][n - 1];
自己对动态规划还是不熟悉
Jz-48. 最长的不含重复字符的子字符串 ⭐⭐
思考
平常解 时间复杂度
关键是每一次index到一个数都需要和当前字符串的字母进行对比,能避免吗?实质是相同字母的最大间距,也可能不是。
1. 动态规划
JZ-50. 第一个只出现一次的字符⭐

1. 哈希表+遍历
先按序遍历一次,统计次数,然后再按序遍历一次,统计第一个出现次数为1的字符
class Solution {
public char firstUniqChar(String s) {
Map<Character, Integer> map = new HashMap<>();
for(int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
Integer nums = map.get(c);
if(nums == null) {
map.put(c, 1);
}else{
map.put(c, ++nums);
}
}
for(int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if(map.get(c) == 1) {
return c;
}
}
return ' '
}
}
注意,这里map的value也可也设置为,只出现一次则为索引值,出现多次则为-1,最终遍历判断
2. 哈希表+队列
主要按FIFO顺序存储出现的元素,那最后肯定希望的是从队列中拿出一个队头元素(首次出现)就行了,不用再遍历一次,因此问题就变成了当队头元素出现两次及以上时,如何将队头元素出队,所以队列中要判断当前元素的出现次数。
- 当元素第一次出现时,先添加进Map中统计并且插入队列中
- 当元素多次出现时,先将统计的值置为-1(表示多次出现),然后再判断队头以及之后的元素是否是单次出现的,如果是的话则需要出队
class Solution {
public char firstUniqChar(String s) {
Map<Character, Integer> map = new HashMap<>();
Queue<Character> queue = new LinkedList<>();
for(int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if(!map.containsKey(c)) {
map.put(c, i);
queue.offer(c);
}else{
map.put(c, -1);
// 关键代码, 比较当前元素是否是多次出现的
while(!queue.isEmpty() && map.get(queue.peek()) == -1) {
queue.poll();
}
}
}
return queue.isEmpty()?' ':queue.poll();
}
}
JZ-54. 二叉搜索树第k大节点 ⭐
思考
递归 ?
中序遍历
class Solution {
int res =0, m =0;
public int kthLargest(TreeNode root, int k) {
m = k;
getMax(root);
return res;
}
public void getMax(TreeNode node){
if(node == null){
return ;
}
getMax(node.right);
if(m == 0){
return ;
}
if(--m == 0){
res = node.val;
}
getMax(node.left);
}
}
时间复杂度 On 空间复杂度 O1
这道题主要一直在纠结递归的返回参数问题,思考的时候没有思考深入, 没有想清楚本质,以后遇到这种问题还是要多想一哈,不过感觉递归还是个人的弱点.....
涉及到二叉搜索树,就要想清楚他的性质,中序遍历是从小到大的排序数组
JZ-56 数组中数字出现的次数 I ⭐⭐
思考
On 时间复杂度 O1 空间复杂度
哈希表肯定用不了 取模算不了 动态规划算不了 双指针 数组肯定是偶数长度的
两次遍历? 排序?
1. My hashTable
public int[] singleNumbers(int[] nums) {
int max = nums[0];
int[] result = {-1,-1};
for(int i = 0;i<nums.length;i++){
if(max<nums[i])
max = nums[i];
}
int[] hash = new int[max*2+2];
for(int i = 0;i<max*2+2;i++){
hash[i] = -1;
}
for(int i = 0;i<nums.length;i++){
int x = nums[i];
if(hash[x*2] != -1){
hash[2*x+1] = x;
}else{
hash[2*x] = x;
}
}
for(int i =0;i<nums.length;i++){
if(hash[2*nums[i]+1] == -1 ){
if(result[0] == -1){
result[0] = nums[i];
}else{
result[1] = nums[i];
}
}
}
return result;
}
居然还不错?
2. My HashMap
public int[] singleNumbers(int[] nums) {
HashMap<Integer,Integer> hashMap = new HashMap();
int[] result = {-1,-1};
for(int i = 0;i<nums.length;i++){
if(hashMap.getOrDefault(nums[i],-1) == -1){
hashMap.put(nums[i],1);
}else{
hashMap.put(nums[i],2);
}
}
for(int i = 0;i<nums.length;i++){
if(hashMap.get(nums[i])==1){
if(result[0] == -1){
result[0] = nums[i];
}else{
result[1] = nums[i];
}
}
}
return result;
}
3. 异或大法
理由: 相同的两个数字异或结果肯定为 0 ,且异或具有交换性
分组:找到不同的a,b不同的位数 进行分组
public int[] singleNumbers(int[] nums) {
int total = 0;
for(int num:nums){
total ^= num;
}
int mask = 1;
while((mask & total) == 0){
mask <<= 1;
}
int a =0 ,b = 0;
for(int num:nums){
if((mask & num) ==0){
a ^= num;
}else{
b ^= num;
}
}
return new int[]{a,b};
}
Jz-63. 股票的最大利润 ⭐⭐
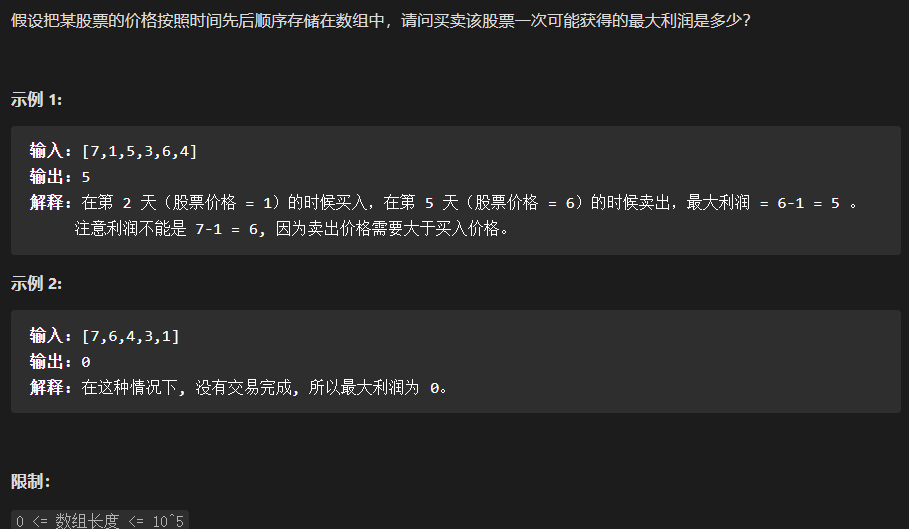
思考
双指针?排序?
前后遍历 O 2N
1. 双指针遍历
public int maxProfit(int[] prices) {
if(prices.length == 0){
return 0;
}
int maxInterval = 0;
int preIndex = 0;
int lasIndex = prices.length - 1;
while(preIndex != lasIndex){
while(lasIndex != preIndex){
if(prices[lasIndex] - prices[preIndex] >maxInterval){
maxInterval = prices[lasIndex] - prices[preIndex];
}
lasIndex --;
}
preIndex ++;
lasIndex = prices.length - 1;
}
return maxInterval;
}
时间复杂度 On*n 空间复杂度 O1
2. 动态规划
核心思想
创建一个数组 dp[i]代表的是i天卖出时的最大收益
又可等于 第i-1天的最大收益 或者 第i天价格 - 前i-1天价格的最低价
public int maxProfit(int[] prices) {
int minValue = Integer.MAX_VALUE;
int profit = 0;
for(int i =0; i<prices.length; i++){
minValue = Math.min(minValue,prices[i]);
profit = Math.max(profit,prices[i]-minValue);
}
return profit;
}
时间复杂度On 空间复杂度O1
还是,多去找通项公式,不一定是符号表达的,能用语言刻画的一样可以
JZ-II-16. 不含重复字符的最长子字符串⭐⭐

1. 暴力
统计从索引为i处开始且符合条件的子串的最大长度,空间复杂度O(n^2)
class Solution {
public int lengthOfLongestSubstring(String s) {
int max = 0;
Map<Character, Integer> map;
for(int i = 0; i < s.length(); i++) {
int temp = 0;
map = new HashMap<>();
for(int j = i; j < s.length(); j++) {
if(map.get(s.charAt(j)) == null) {
temp++;
map.put(s.charAt(j), 1);
}else{
break;
}
}
max = Math.max(temp, max);
}
return max;
}
}
2. 滑动窗口-队列+哈希
还不错,能把这个想出来。
思路就是维通过先进先出维护一个队列、当前队列对应的哈希表、队列中队头元素的索引,队列中时刻维护着当前遍历长度下符合条件的最长子串,通过一次遍历就能解决问题。时间复杂度比解法1更好一点
- 当前元素不在哈希表中(说明队列中肯定也没有), 则该元素入队并添加到哈希表中,Value为索引
- 当前元素在哈希表中(说明队列中肯定有该元素), 则将队头到与当前字符重复的那个字符所在的队列区间清空(同时清空哈希表), 再将当前元素添加到队列与哈希表中。
为什么这里可以使用滑动窗口的思路?
递增性⤴️
如果我们依次递增地枚举子串的起始位置,那么子串的结束位置也是递增的!这里的原因在于,假设我们选择字符串中的第 kkk 个字符作为起始位置,并且得到了不包含重复字符的最长子串的结束位置为 rk。那么当我们选择第 k+1个字符作为起始位置时,首先从 k+1到 rk 的字符显然是不重复的,并且由于少了原本的第 k 个字符,我们可以尝试继续增大 rk ,直到右侧出现了重复字符为止。这样一来,我们就可以使用「滑动窗口」来解决这个问题了:
摘自力扣官方题解
public int lengthOfLongestSubstring(String s) {
Queue<Character> queue = new LinkedList<>();
Map<Character, Integer> map = new HashMap<>();
int max = 0;
int curIndex = 0;
for(int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if(map.get(c) == null) {
map.put(c, i);
queue.offer(c);
}else{
max = Math.max(queue.size(), max);
int num = map.get(c);
while(curIndex <= num) {
map.remove(queue.poll());
curIndex++;
}
i--;
}
}
return Math.max(queue.size(), max);
}
优化
尝试考虑不使用Queue而使用左右指针维护,Map改为HashSet
问题
这里自己犯了一个很经典的问题,在写代码时,while判断时,为了代码简洁,使用了第一种写法,但最终却一直报超时。
// Solution 1
while(curIndex <= num) {
map.remove(queue.poll());
curIndex++;
}
// Solution 2
while(curIndex++ <= num) {
map.remove(queue.poll());
}
这其实就是在while循环中使用 自增/减符号不当可能引发的错误❎。例如当curIndex = 1, num = 3时,使用第一种方式最终curIndex结果为 4, 而第二种结果方式为5.原因很简单,因为在第一种方式里,判断时只要条件不满足就会退出循环,而第二种方式里,条件不满足会退出循环并且还会对curIndex自增,所以这就造成了curIndex比预期值多了1.
JD-17.09. 第K个数 ⭐⭐
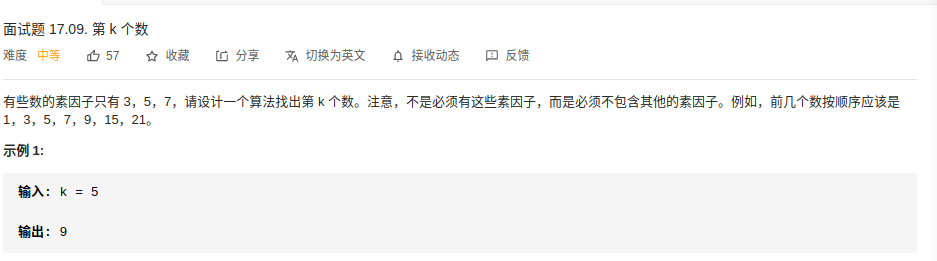
思考
递归、动态规划 无果
1. 动态规划
public int getKthMagicNumber(int k) {
int[] numList=new int[k];
int p3=0,p5=0,p7=0;
numList[0]=1;
for(int i=1;i<k;i++){
numList[i]=Math.min(Math.min(numList[p3]*3,numList[p5]*5),numList[p7]*7);
if(numList[i]==numList[p3]*3) p3++;
if(numList[i]==numList[p5]*5) p5++;
if(numList[i]==numList[p7]*7) p7++;
}
return numList[k-1];
}

这是合并子序列问题,当这种可选择的,可分成不同数组的I问题,可以采用合并子序列方法,多索引判断
面试-17.10. 主要元素 ⭐
思考
- 要求在On的时间复杂度内,肯定是一次遍历。最开始尝试用“最近出现最多次”的方法来统计,但最后发现不可行。但想不到其他的办法了
1. Boyer-Moore 投票算法
自己想的“最近出现最多次”方法的原理与之基本相同,但关键点在于没有对候选元素进行再一次验证。也就是当面对[1,2,3]和 [3,2,3]的情况时想不到处理的对策,这也是自己算法的问题所在,只做了第一步却没有做第二步。
int majorityElement(int* nums, int numsSize){
int cur_num = nums[0];
int count = 0;
for(int i = 0; i < numsSize; i++) {
// 优化,如果出现size / 2 + 1次,则说明就是主元素
if(count > numsSize / 2) {
return cur_num;
}
if(cur_num == nums[i]) {
count++;
}else{
count--;
}
// count为0时,即候选数不间断出现的次数与这之间出现其他不同的数的次数抵消,则替换候选数
if(count <= 0) {
cur_num = nums[i];
count = 1;
}
}
count = 0;
// 验证候选数是否符合条件
for(int i = 0; i < numsSize; i++) {
if(nums[i] == cur_num) {
count++;
}
}
return count > numsSize / 2? cur_num : -1;
}
什么当数组中存在主要元素时,Boyer-Moore 投票算法可以确保得到主要元素?
LeetCode: Boyer-Moore投票算法中,遇到相同的数则将 count 加 1,遇到不同的数则将 count 减 1。根据主要元素的定义,主要元素的出现次数大于其他元素的出现次数之和,因此在遍历过程中,主要元素和其他元素两两抵消,最后一定剩下至少一个主要元素,此时candidate 为主要元素,且 count≥1。
总结
- 验证也是设计算法时一个重要的环节 ⚠️ ,再次遍历不会影响On的时间复杂度
1. 两数之和 ⭐
先审题, 两个整数,返回数组下标,给出的数组不是排序的,返回的数组是排序的?
回过头才发现忽略的因素: 数组是否有相同元素?
思路
- 二分?
- 排序后找?
我的代码:
1. 双头指针
int[] result = new int[2];
int i,j;
//一个向前 一个向后,避免重复查找
for(i = 0; i < nums.length;i++){
for(j = nums.length-1; j>i; j--){
if(nums[i]+nums[j] == target){
result[0] = i;
result[1] = j;
return result;
}
}
}
return null;
时间复杂度 O(N2) 空间复杂度 O(1)
2. 哈希表
确实,最开始想到了郑老板出题的时候这个,只是怕放入map集合又会消耗一定的时间,哎.....
Map map = new HashMap<Integer,Integer>();
int j ;
for(int i =0; i<nums.length; i++){
j = (int)map.getOrDefault(nums[i],-1);
if(j != -1){
return new int[]{j,i};
}
map.put(target - nums[i] , i);
}
return null;
时间复杂度 : O(N) 空间复杂度 O(N) 哈希表的开销
这里由于哈希表 的get方法是 O(1)的开销,所以考虑哈希表的方式直接查找,精妙之处在与其索引key的灵活使用
4. 寻找两个正序数组的中位数 ⭐⭐⭐
思路
- 暴力解法:将两个数组合二为一然后直接取中位数即可,时间、空间复杂度O(m + n)
- 基于数组是正序的来思考
1. 双指针 (未达标)
并不需要得到整个数组再去用O1的时间找,只需要在定位到中位数,即哪个数在数组,也就是位于 (m + n) / 2 或者 (m + n) / 2与 (m + n) / 2 - 1的位置,在此之前数组都是正序排序的。所以只需要在两个数组中筛选出前(m + n) / 2个数即可。
代码不够优雅,有待改进。
double findMedianSortedArrays(int* nums1, int nums1Size, int* nums2, int nums2Size){
int i = 0;
int j = 0;
int index = 0;
double arr[2];
while(i + j <= (nums1Size + nums2Size) / 2) {
// 用于保存(nums1Size + nums2Size) / 2的元素到另一个变量中
if(i + j == (nums1Size + nums2Size) / 2) {
index = 1;
}
if(i >= nums1Size) {
arr[index] = nums2[j++];
}
else if(j >= nums2Size) {
arr[index] = nums1[i++];
}
else if(nums1[i] > nums2[j]) {
arr[index] = nums1[i] < nums2[j] ? nums1[i]:nums2[j];
j++;
}else{
arr[index] = nums1[i] < nums2[j] ? nums1[i]:nums2[j];
i++;
}
}
// 判断中位数是一个还是两个
if((nums1Size + nums2Size) % 2 == 0) {
return (double)((arr[0] + arr[1]) / 2.0);
}else{
return arr[1];
}
}
时间复杂度O(m + n)

2. 二分查找
可以思考一种在Olog时间复杂度内到方法,巧妙
6. Z 字形变换⭐⭐
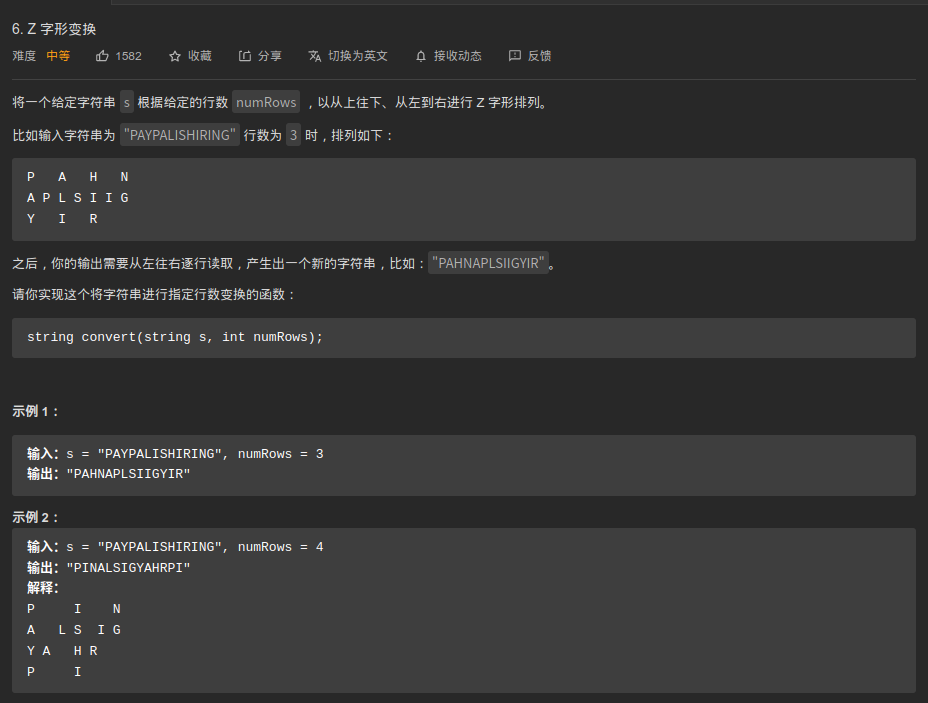
审题
- Z字形排序主要针对列 numRow限定行数,多的行数可能会增加难度
- 可能的数据结构、数学公式?
- 分析:
- 简单:先创建二维字符矩阵,然后根据填好的矩阵按照次序输出,但这样的空间复杂度高
- 进阶:按照规律直接划分一维的数组
- 做后反思点:
- row不为1和n和为1和n的时候的特殊情况,一次存在2个点和只存在一个点
1. 暴力
先划分好二维字符矩阵,然后再按照Z字形排序依次填入矩阵中,最后从矩阵中依照行列顺序读就行了。
缺点:耗费O(numRow * actCol)的空间复杂度
2. 数学公式
一维字符数组本来不用排到二维矩阵中就有的Z字形逻辑,逻辑上通过等差数列也可以得到
public String convert(String s, int numRows) {
// 特殊情况判断,避免后面除法出现分母为0的情况
if(numRows == 1) {
return s;
}
StringBuilder sb = new StringBuilder();
int actCol = s.length() / (numRows * 2 - 2) + 1;
int n = numRows;
int curRow = 1;
int i = 1;
while(curRow <= numRows) {
if(curRow == 1 || curRow == numRows) {
for(i = 0; i < actCol; i++) {
if((curRow + 2 * i * (n-1)) <= s.length()){
sb.append(s.charAt((curRow + (2 * i * (n-1))) - 1));
}
}
curRow++;
}else{
if(curRow <= s.length()) {
sb.append(s.charAt(curRow - 1));
}
for(i = 1; i <= actCol; i++) {
if(curRow + 2 * i * (n-1) - (curRow-1) * 2<= s.length()){
sb.append(s.charAt(curRow + 2 * i * (n-1) - (curRow-1) * 2 - 1));
}
if(curRow + 2 * i * (n-1)<= s.length()){
sb.append(s.charAt(curRow + 2 * i * (n-1) - 1));
}
}
curRow++;
}
}
return sb.toString();
}
还不错!On的时间复杂度和空间复杂度,sb节省了一定的时间
3. 顺序遍历 分行存储 (转)
思路就是按照顺序遍历,通过索引flag区分到哪一行了,到Z字形转折点时就flag--,非常的巧妙。思路真的是非常的好想,为什么我开始没有想到这么好滴思路?感觉自己一下就跳过顺序遍历这种想法了,可能因为觉得分行存储不好做吧(但实际还是可以的)
class Solution {
public String convert(String s, int numRows) {
if(numRows < 2) return s;
List<StringBuilder> rows = new ArrayList<StringBuilder>();
for(int i = 0; i < numRows; i++) rows.add(new StringBuilder());
int i = 0, flag = -1;
for(char c : s.toCharArray()) {
rows.get(i).append(c);
if(i == 0 || i == numRows -1) flag = - flag;
i += flag;
}
StringBuilder res = new StringBuilder();
for(StringBuilder row : rows) res.append(row);
return res.toString();
}
}
// 作者:jyd
// 链接:https://leetcode-cn.com/problems/zigzag-conversion/solution/zzi-xing-bian-huan-by-jyd/
但因为使用了多个SB,所以这里的空间占用率略高,还存在多个sb合并的合并的情况,所以时间复杂度也相对较高,但是思路确实是非常的清晰的。
反思
还是做题的时候的一些问题:
- 寄... 花了很多时间,中间卡了很久,结果是因为自己做题是设了个n,默认的是numRows,但应用的时候没有写,导致查了半天bug。还是写的时候严谨一点,尽可能用它给的参数,否则就自己提前说明好来
- 数学太撇,等差公式还看错了.....
- 还有charAt和自己写的row起始索引不一致导致后续更换问题,本来是0开始,我自己为了方便从1开始,但后续就需要-1,如果没发现这个问题的话还会有错误
7. 整数反转 ⭐⭐
Time : 2022 / 4 / 6 9 :46
TAG : Overflow / Decimal
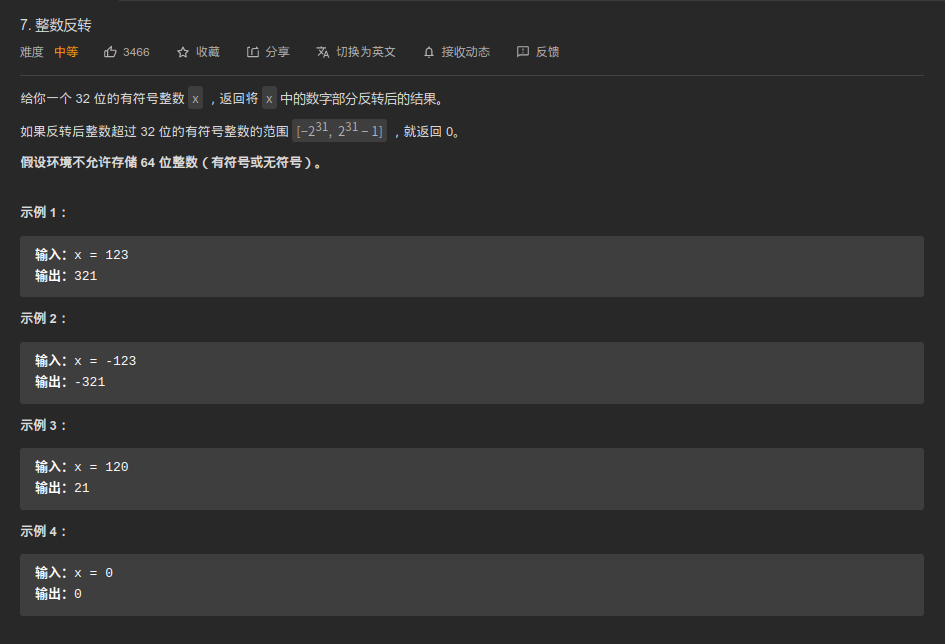
审题
- 翻转后整数超过32位signed 范围就返回0
- 环境不准存储64位整数
- 思路:
- 直接:
- 十进制按位取,然后再拼凑
- 位运算?
- 直接:
1. 十进制按位计算
按十进制取位,然后再反过来乘,组成新的十进制。但需要注意以下问题:
- 负数取模问题:temp取绝对值,因为负数的符号影响之后的加减法
- 如何正确判断溢出的情况?
冗余:我这里ArrayList完全没必要,因为后面的计算顺序是从后往前算,其实也可以从前往后算
public int reverse(int x) {
int temp = Math.abs(x);
List<Integer> list = new ArrayList<>();
int res = 0;
int flag = 0;
int paw = 1;
while(temp / 10 != 0) {
list.add(temp % 10);
temp = temp / 10;
}
list.add(temp % 10);
int i = list.size();
while(i > 0) {
int tmp = list.get(--i);
if(i == list.size() - 1 && tmp == 0) {
flag = 1;
}else{
// Overflow detection
if(res > tmp * paw + res) {
return 0;
}
res = (tmp * paw) +res;
flag = 0;
paw *= 10;
}
}
// overflow detection.not rigorous
if(res % 10 != list.get(list.size() - 1)) {
return 0;
}
if(x < 0){
return -Math.abs(res);
}
return res;
}
O(n)的时间复杂度,加减法和模10耗时
题解的优化
官方题解的优化确实比我写的要好得多,用 < Integer.xxx_VALUE / 10 来判断是否溢出,这种方法非常的简便快速
public int reverse(int x) {
int rev = 0;
while (x != 0) {
if (rev < Integer.MIN_VALUE / 10 || rev > Integer.MAX_VALUE / 10) {
return 0;
}
int digit = x % 10;
x /= 10;
rev = rev * 10 + digit;
}
return rev;
}
注意点
题解的方法跟我方法差距这么大主要是有一个原因:
当顺序取模10的数,即从低到高位,则
rev = rev * 10 + digit;当逆序取模10的数,即从高到低位,则
res = (digit * paw) +res;
两种思路不一样,产生的解决方法也就不一样,第一种的解决方法能在一次遍历内就解决,而我这一种要先遍历一次并存储,再从集合中去取,经历两次运算和集合操作,自然就要慢一点。
所以还是对一种已知方法就数学问题上要思考一下有没有其他的方式能得到这个值,多思考几种方案取最简洁的那一种
2. 字符串反转
突发奇想,用类库进行字符串反转,再Catch Exception去捕获溢出时转换的异常,比较慢但是算是一种方法.......
public int reverse(int x) {
String s = String.valueOf(Math.abs(x));
s = new StringBuilder(s).reverse().toString();
int i = 0;
for(i = 0 ; i < s.length() ;i++) {
if(s.charAt(i) != '0') {
break;
}
}
// 截取尾数连续为0的部分
s=s.substring(i,s.length());
if(s.length() < 1) {
return 0;
}
int res = 0;
try{
res = Integer.parseInt(s);
}catch(NumberFormatException e) {
return 0;
}
if(x < 0) {
return 0-res;
}
return res;
}
11. 盛最多水的容器 ⭐⭐
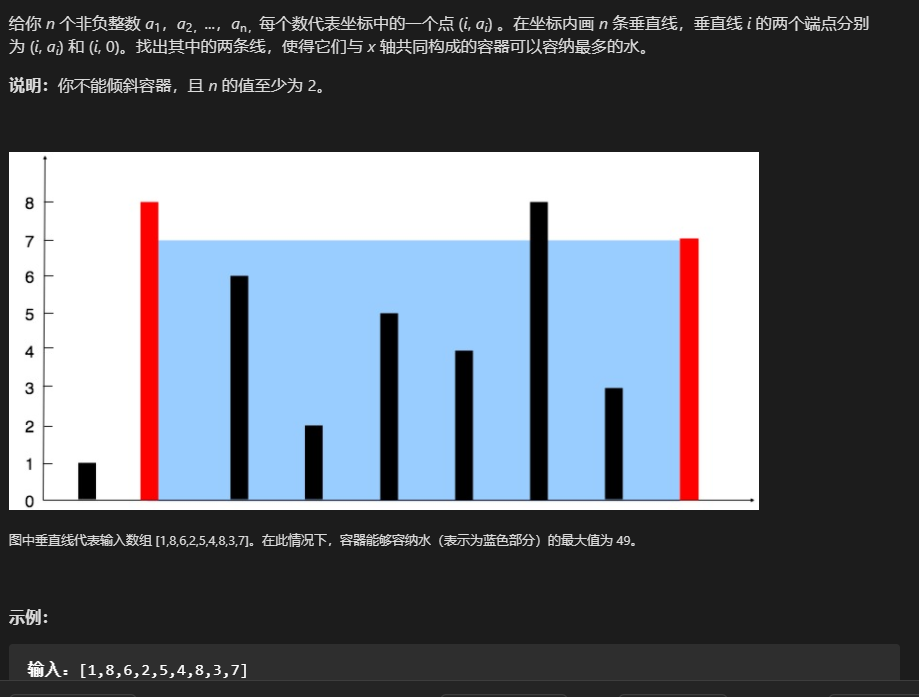
1. 暴力(超时)
public int maxArea(int[] height) {
int final_max = 0;
for(int i = 0; i < height.length; i++) {
int max = 0;
for(int j = 0; j < height.length; j++) {
int min = Math.min(height[i], height[j]);
int gap = Math.abs(i - j);
max = Math.max(max, min*gap);
}
final_max = Math.max(final_max, max);
}
return final_max;
}
2. 一次遍历(转)
- 若向内 移动短板 ,水槽的短板 min(h[i], h[j]) 可能变大,因此下个水槽的面积 可能增大 。
- 若向内 移动长板 ,水槽的短板 min(h[i], h[j]) 不变或变小,因此下个水槽的面积 一定变小 。
class Solution {
public int maxArea(int[] height) {
int i = 0, j = height.length - 1, res = 0;
while(i < j) {
res = height[i] < height[j] ?
Math.max(res, (j - i) * height[i++]):
Math.max(res, (j - i) * height[j--]);
}
return res;
}
}
// 作者:Krahets
// 链接:https://leetcode.cn/problems/container-with-most-water/solutions/11491/container-with-most-water-shuang-zhi-zhen-fa-yi-do/

12. 整数转罗马数字 ⭐⭐

我的代码:
HaspMap 存储键值对 判断
static String getOne(int n){
StringBuilder stringBuilder=new StringBuilder("");
int a[]={1,4,5,9,10,40,50,90,100,400,500,900,1000};
int i=a.length-1;
Map hashMap=new HashMap<Integer,String>();
hashMap.put(1,"I"); hashMap.put(4,"IV"); hashMap.put(9,"IX");
hashMap.put(40,"XL"); hashMap.put(90,"XC");hashMap.put(400,"CD");
hashMap.put(900,"CM"); hashMap.put(5,"V"); hashMap.put(10,"X");
hashMap.put(50,"L");hashMap.put(100,"C"); hashMap.put(1000,"M");
while(i>=0){
if(n/a[i]>0){
n=n-a[i];
stringBuilder.append(hashMap.get(a[i]));
}else{
i--;
}
}
return String.valueOf(stringBuilder);
}

贪心法int String 基本数组 对应存储
public String intToRoman(int num) {
StringBuilder stringBuilder=new StringBuilder("");
int[] a = {1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1};
String[] s = {"M","CM","D","CD","C","XC","L","XL","X","IX","V","IV","I"};
int i=0;
while(i<a.length){
if(num>=a[i]){
num=num-a[i];
stringBuilder.append(s[i]);
}else{
i++;
}
}
return String.valueOf(stringBuilder);
}

思考
- 对于判断 和 输出对于字符的思路,我的思路上与题设大体一致
- 不能解决 4 -9 的问题,就只能存储进数组中,通过索引解决
HashMap 中的get方法时间复杂度是否为O(1)?
在hash不发生冲突的情况下, 是O(1),也就是说,最优情况才是O(1),没有第二种方法直接建立int a[] 和String s[]的直接对应联系来的 快
15. 三数之和 ⭐⭐

审题
- 一个三元组中的元素之间不可以有重复,且三元组组与组之间不可有重复
- 思路:
- 三个元素相加=0可以简化为两个数之和等于第三个数,
所以能尽快验证前两个数之和是否在第三个数中是极好的(O(1)时间复杂度), 所以考虑到用哈希来缓存 - 方案不可行,因为很难解决三元组组间不重复问题
- 三个元素相加=0可以简化为两个数之和等于第三个数,
1. 排序+双指针 (R)
现在已知通过暴力三重循环能够解决问题,但如何将问题的时间复杂度从O(N3)优化到O(N2)?
外层循环肯定是不变的,那也就是针对当前索引的元素,如何通过一次遍历找到数组中其他两个元素,使其两元素之和等于这个元素的相反数?
所以可以通过先将数组排序(关键),然后在内循环中使用双指针来同步进行.双指针一头在首一头在尾,通过两指针元素之和与外循环元素相反数比较,从而判断此时该左指针右移(三数之和小于0)还是右指针左移(三数之和大于0),两指针逐步趋于目标值,就能通过一次遍历找出相符合的所以另外两个元素
同时注意细节,这里要三元组组间不重复,所以要排除内外循环当前元素与前一个位置相同的情况
所以能够将时间复杂度为O(N3)的暴力解法优化为时间复杂度为O(N2) 空间复杂度为O(logN)的算法(排序时二分递归占用空间)
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> res = new ArrayList<>();
Arrays.sort(nums);
for(int i = 0; i < nums.length; i++) {
// 针对外层循环, 避免重复的问题
if(i > 0 && nums[i] == nums[i - 1]) {
continue;
}
int l = i + 1;
int r = nums.length - 1;
while(l < r) {
// 避免重复的问题, 只用判断左/右一种情况即可
if(l != i + 1 && nums[l] == nums[l-1]) {
l++;
continue;
}
if(nums[l] + nums[r] + nums[i] == 0) {
List<Integer> cur = new ArrayList<>();
cur.add(nums[i]);
cur.add(nums[l]);
cur.add(nums[r]);
res.add(cur);
// 不要忘记自增左或右指针
l++;
}else if(nums[l] + nums[r] + nums[i] > 0) {
r--;
}else{
l++;
}
}
}
return res;
}
}
17. 电话号码的字母组合 ⭐⭐
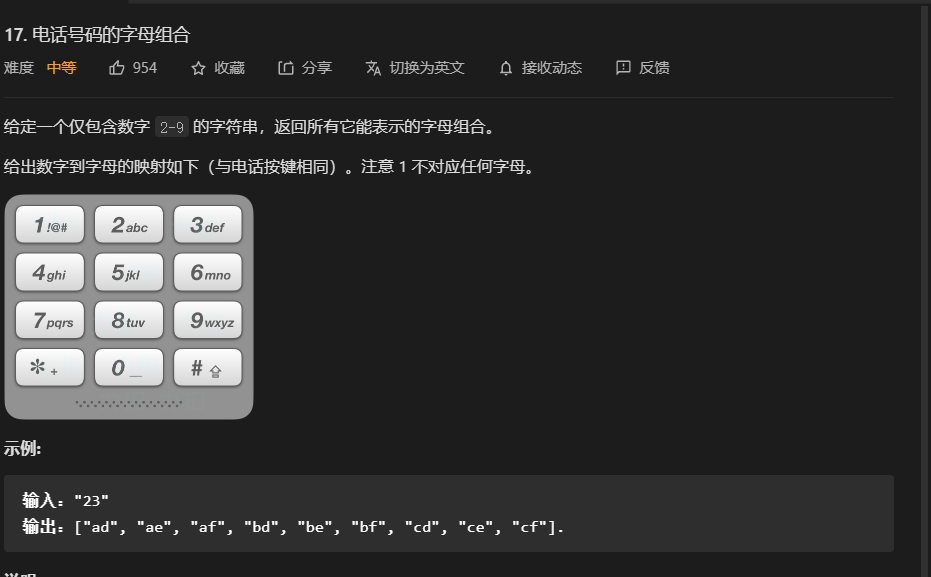
我的代码:
String类型的迭代
private String letterMap[] = {
" ", //0
"", //1
"abc", //2
"def", //3
"ghi", //4
"jkl", //5
"mno", //6
"pqrs", //7
"tuv", //8
"wxyz" //9
};
private ArrayList<String> res;
List<String> letterCombinations(String digits){
if(digits.equals(""))
return list;
else{
getString(digits,0,"");
return list;
}
}
void getString(String digits,int index,String tmp){
if(index==digits.length()) {
list.add(tmp);
return ;
}
char c=digits.charAt(index);
String letter=arrstr[c-'0'];
for(int i=0;i<letter.length();i++){
getString(digits,index+1,tmp+letter.charAt(i));
}
}
StringBuilder 实现的迭代
class Solution {
//一个映射表,第二个位置是"abc“,第三个位置是"def"。。。
//这里也可以用map,用数组可以更节省点内存
String[] letter_map = {" ","*","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
public List<String> letterCombinations(String digits) {
//注意边界条件
if(digits==null || digits.length()==0) {
return new ArrayList<>();
}
iterStr(digits, new StringBuilder(), 0);
return res;
}
//最终输出结果的list
List<String> res = new ArrayList<>();
//递归函数
void iterStr(String str, StringBuilder letter, int index) {
//递归的终止条件,注意这里的终止条件看上去跟动态演示图有些不同,主要是做了点优化
//动态图中是每次截取字符串的一部分,"234",变成"23",再变成"3",最后变成"",这样性能不佳
//而用index记录每次遍历到字符串的位置,这样性能更好
if(index == str.length()) {
res.add(letter.toString());
return;
}
//获取index位置的字符,假设输入的字符是"234"
//第一次递归时index为0所以c=2,第二次index为1所以c=3,第三次c=4
//subString每次都会生成新的字符串,而index则是取当前的一个字符,所以效率更高一点
char c = str.charAt(index);
//map_string的下表是从0开始一直到9, c-'0'就可以取到相对的数组下标位置
//比如c=2时候,2-'0',获取下标为2,letter_map[2]就是"abc"
int pos = c - '0';
String map_string = letter_map[pos];
//遍历字符串,比如第一次得到的是2,页就是遍历"abc"
for(int i=0;i<map_string.length();i++) {
letter.append(map_string.charAt(i));
//如果是String类型做拼接效率会比较低
//iterStr(str, letter+map_string.charAt(i), index+1);
iterStr(str, letter, index+1);
//这个方法保证了每一次大循环后得到的stringbuilder都是新的
//注意: 这里的删除方法很重要!!
letter.deleteCharAt(letter.length()-1);
}
}
}

思考
StringBuilder 确实操作比 String类型快很多很多,且在 空间占用上也远远低于 String
这还得归结于String 相加时 总会新分配一个String对象进行赋值
21. 合并两个有序列表 ⭐
1. 迭代
/*
题目给的是: 有 序 的数组,这点很重要
*/
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode nodehead = new ListNode(-1);
ListNode pre = nodehead;
// 理解这里pre=nodehead 的指向问题
while (l1 != null && l2 != null) {
try {
if (l1.val <= l2.val) {
pre.next = l1; // 这里的两步都能想到
l1 = l1.next;
} else {
pre .next= l2;
l2 = l2.next;
}
// 这里注意! 关键点 是指针节点后移的步骤
// 那pre之前的数呢? ---传给nodehead了
pre = pre.next;
}catch (NullPointerException e){
}
}
//抓一下最后几个节点,可能不止一个节点,但他是有序的,就无妨了
pre.next=l1==null?l2:l1;
return nodehead.next;
/**
* 时间复杂度O(n+m) 空间复杂度O(1) (pre 和nodepre作为变量)
*/
}

2. 递归
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if(l1==null)
return l2;
else if(l2==null)
return l1;
//到这里都没问题
else if(l1.val<=l2.val) {
//此处 总爱 直接return一个 函数方法体 其实是不对的 ,具体得到的是谁呢?
// 用 node.next能够实现对元素的保存
l1.next = mergeTwoLists(l1.next, l2);
return l1;
}
else{
l2.next = mergeTwoLists(l1, l2.next);
return l2;
}
/**
* 时间复杂度O(n+m) 空间复杂度O(m+n) (递归函数的调用)
所以 执行结果内存消耗稍微慢于 迭代
*/
}

分析:
自己做的时候,开始是都想到了这两种算法,不过后来总觉得哪里行不通,就放弃了递归,采用迭代。分析问题的原因:
- 问题用那种方法解决?
- 从头部解决: --------迭代
- 用头元素记录 ,标兵元素去移动
- 从尾部解决: --------递归
- 为了得到保存结果 用next指针继续下一次判断
- 从头部解决: --------迭代
- 两者的关键点 都是 巧妙的使用 next指针
26. 删除排序数组中的重复项 ⭐
1. 暴力三循环 --解非排序数组
/**
* 删除数组中重复元素的
* 分析: 造成 时间复杂度高的步骤: 判断 之后的元素是否相等和 移动数组
*/
// for 三层循环来做 算法不稳定 O(N3)/Ok(1)
static int deleteSameNode(int[] nums){
int total=nums.length;
// 设置total 用于 循环体中 避免重复判断
for(int i=0;i<total;i++){
for(int j=i+1;j<total;j++){
if(nums[i]==nums[j]) {
total-=1;
for(int k=j;k<total;k++){
nums[k]=nums[k+1];
}
j--; //注意这里的 j--
}
}
}
return total;
}
注意点:
- j-- :避免多个重复的数在一起而被漏掉
- total作为循环判断的依据: 避免多个重复的数在一起而被漏掉 或者 重复判断了移动到末尾的数字
2. 双指针单循环 --- 解排序数组
static int deleteSameNode_2(int[] nums) {
int i = 0;
for (int j = 1; j < nums.length; j++) {
if(nums[i]!=nums[j]){
i++;
nums[i]=nums[j];
}
}
return i+1;
}

反思
这里我思考的时候 ,没有看题目要求, 直接按照一般的数组来解决了,其实 题目给的 有序数组 ,双循环再想到单循环双指针 ,是非常好解决的。此处也提供了一种思路, 先将 数组 有序化 ,再通过这种方式 进行O(n) 的运算
28. 实现strStr() ⭐⭐
Time : 2022 / 3 / 26 10 : 23
TAG : KMP、迭代
审题
- 返回匹配的子字符串在母字符串中第一次出现的位置
- 母串长度为n 字符串长度为m
1. 暴力迭代
在母串中依次查找,时间复杂度O(nm)
2. KMP
关于KMP,在字符串匹配中的应用是十分重要的,因为它把O(mn)的时间复杂度降低至O(m + n)
Knuth-Morris-Pratt 算法,简称 KMP 算法,由 Donald Knuth、James H. Morris 和 Vaughan Pratt 三人于 1977 年联合发表
KMP的核心步骤:
- 根据目标子串生成next数组(重点)
- 在母串中依据目标子串和next数组进行查找
public int strStr(String haystack, String needle) {
if(needle.equals("")) {
return 0;
}else if(haystack.equals("")) {
return -1;
}
int[] next = kmp_gen_next(needle);
int res = is_son_str(haystack, needle, next);
return res;
}
public int is_son_str(String s, String son, int[] next) {
int i = 1;
int j = 1;
while(i <= s.length() && j <= son.length()) {
if(j == 0 || s.charAt(i-1) == son.charAt(j-1)) {
i++;
j++;
}else{
j = next[j-1];
}
}
if(j > son.length()){
return i - j;
}
return -1;
}
public int[] kmp_gen_next(String s) {
int[] next = new int[s.length()];
int i = 1;
int j = 0;
next[0] = 0;
while(i < next.length) {
if(j == 0 || s.charAt(i - 1) == s.charAt(j - 1)) {
i++;
j++;
next[i-1] = j;
}else{
j = next[j-1];
}
}
return next;
}
优化
针对next数组优化,因为如果father_str[i] != son_str[j] 且 son_str[j] == son_str[next[j]]时,就会出现不必要的重复判断,因为之前判断两者不相等,而转化j后再去判断,(但son_str[j] == son_str[next[j]])所以两者肯定还是不相等,就优化了next数组
public int[] kmp_gen_next_modified(String s) {
int[] next = new int[s.length()];
int i = 1;
int j = 0;
next[0] = 0;
while(i < next.length) {
if(j == 0 || s.charAt(i - 1) == s.charAt(j - 1)) {
i++;
j++;
if(s.charAt(i - 1) != s.charAt(j - 1))
next[i - 1] = j;
else
next[i-1] = next[j - 1];
}else{
j = next[j-1];
}
}
return next;
}
不明显,可能是生成next时多了一些判断?

二刷-C语言版本
自己觉得KMP难理解的点(配合图来理解):
- 先理解前缀和后缀,KMP是通过子串的前后缀来进行线性判断的。也就是说,如果子串有相同的最长前、后缀,则就可以进行移位比较
- 接下来,如何计算这个最长的前后缀?问题的关键也就变成了计算next数组了,那next数组是什么?next数组是指示截止当前元素为止,当前长度的数组最长前后缀的长度是多少?例如abcabcd,d处的数值便是3(因为有最长前后缀abc)。计算next数组时的一个难点,也是我认为比较难以理解的一个地方:在比较计算第k个索引元素的值时。先看前一个元素的值,也就是看到前一个数为止当前数组的最大前后缀,若值为m。
- 则比较第m+1个元素与当前元素是否相等,如果相等,就说明到当前元素为止,数组能构成一个更长的前后缀(这里可以画图理解),所以当前元素的值=前一个元素值+1
- 如果不想等的话,则要去找次长的前后缀,然后比较次长的前缀 和 加了新元素的后缀是否相等,如果找到了就等于次长前缀长度 + 1,如果没找到,就重复这个过程,直到没有最长前后缀,此时当前元素的值为0(也就是没有最长前后缀)。
int * genNext(char * needle, int length) {
int *next = (int *) calloc(length, sizeof(int));
int i = 1;
int cur_hop = 0;
while(i < length) {
if(needle[i] == needle[cur_hop]) {
cur_hop++;
next[i] = cur_hop;
i++;
}else{
if(cur_hop == 0) {
next[i] == 0;
i++;
}
else{
cur_hop = next[cur_hop - 1];
}
}
}
return next;
}
int strStr(char * haystack, char * needle){
int i, j = 0;
int length = strlen(needle);
int out_length = strlen(haystack);
int *next = genNext(needle, length);
while(i < out_length) {
if(haystack[i] == needle[j]){
j++;
i++;
}else if(j > 0){
j = next[j - 1];
}else{
i++;
}
if(j >= length) {
return i - j;
}
}
return -1;
}

29. 两数相除 ⭐⭐
Time: 2021 10 12 4:06pm
审题
- 不得使用* / mod,也就是说+ - 位运算都可以用、
- 返回[商]
- 除数不为0
- 可以为负数
- 排除递归、dp...
1. 暴力
2. 二分查找(转)
- 先把特殊情况罗列
- 因为溢出的可能,所以都取成负数
- 在判断溢出时用负数和移动不等式两边去进行巧妙判断
class Solution {
public int divide(int dividend, int divisor) {
// 考虑被除数为最小值的情况
if (dividend == Integer.MIN_VALUE) {
if (divisor == 1) {
return Integer.MIN_VALUE;
}
if (divisor == -1) {
return Integer.MAX_VALUE;
}
}
// 考虑除数为最小值的情况
if (divisor == Integer.MIN_VALUE) {
return dividend == Integer.MIN_VALUE ? 1 : 0;
}
// 考虑被除数为 0 的情况
if (dividend == 0) {
return 0;
}
// 一般情况,使用二分查找
// 将所有的正数取相反数,这样就只需要考虑一种情况
boolean rev = false;
if (dividend > 0) {
dividend = -dividend;
rev = !rev;
}
if (divisor > 0) {
divisor = -divisor;
rev = !rev;
}
int left = 1, right = Integer.MAX_VALUE, ans = 0;
while (left <= right) {
// 注意溢出,并且不能使用除法
int mid = left + ((right - left) >> 1);
boolean check = quickAdd(divisor, mid, dividend);
if (check) {
ans = mid;
// 注意溢出
if (mid == Integer.MAX_VALUE) {
break;
}
left = mid + 1;
} else {
right = mid - 1;
}
}
return rev ? -ans : ans;
}
// 快速乘
public boolean quickAdd(int y, int z, int x) {
// x 和 y 是负数,z 是正数
// 需要判断 z * y >= x 是否成立
int result = 0, add = y;
while (z != 0) {
if ((z & 1) != 0) {
// 需要保证 result + add >= x
if (result < x - add) {
return false;
}
result += add;
}
if (z != 1) {
// 需要保证 add + add >= x
if (add < x - add) {
return false;
}
add += add;
}
// 不能使用除法
z >>= 1;
}
return true;
}
}

3. 类二分查找(转)
class Solution {
public int divide(int dividend, int divisor) {
// 考虑被除数为最小值的情况
if (dividend == Integer.MIN_VALUE) {
if (divisor == 1) {
return Integer.MIN_VALUE;
}
if (divisor == -1) {
return Integer.MAX_VALUE;
}
}
// 考虑除数为最小值的情况
if (divisor == Integer.MIN_VALUE) {
return dividend == Integer.MIN_VALUE ? 1 : 0;
}
// 考虑被除数为 0 的情况
if (dividend == 0) {
return 0;
}
// 一般情况,使用类二分查找
// 将所有的正数取相反数,这样就只需要考虑一种情况
boolean rev = false;
if (dividend > 0) {
dividend = -dividend;
rev = !rev;
}
if (divisor > 0) {
divisor = -divisor;
rev = !rev;
}
List<Integer> candidates = new ArrayList<Integer>();
candidates.add(divisor);
int index = 0;
// 注意溢出
while (candidates.get(index) >= dividend - candidates.get(index)) {
candidates.add(candidates.get(index) + candidates.get(index));
++index;
}
int ans = 0;
// 没看懂
for (int i = candidates.size() - 1; i >= 0; --i) {
if (candidates.get(i) >= dividend) {
ans += 1 << i;
dividend -= candidates.get(i);
}
}
return rev ? -ans : ans;
}
}
4. 递归(转)
感觉这个比上面的好懂一点
举个例子:11 除以 3 。
首先11比3大,结果至少是1, 然后我让3翻倍,就是6,发现11比3翻倍后还要大,那么结果就至少是2了,那我让这个6再翻倍,得12,11不比12大,吓死我了,差点让就让刚才的最小解2也翻倍得到4了。但是我知道最终结果肯定在2和4之间。也就是说2再加上某个数,这个数是多少呢?我让11减去刚才最后一次的结果6,剩下5,我们计算5是3的几倍,也就是除法,看,递归出现了。说得很乱,不严谨,大家看个大概,然后自己在纸上画一画,或者直接看我代码就好啦!
class Solution {
public:
int divide(int dividend, int divisor) {
if(dividend == 0) return 0;
if(divisor == 1) return dividend;
if(divisor == -1){
if(dividend>INT_MIN) return -dividend;// 只要不是最小的那个整数,都是直接返回相反数就好啦
return INT_MAX;// 是最小的那个,那就返回最大的整数啦
}
long a = dividend;
long b = divisor;
int sign = 1;
if((a>0&&b<0) || (a<0&&b>0)){
sign = -1;
}
a = a>0?a:-a;
b = b>0?b:-b;
long res = div(a,b);
if(sign>0)return res>INT_MAX?INT_MAX:res;
return -res;
}
int div(long a, long b){ // 似乎精髓和难点就在于下面这几句
if(a<b) return 0;
long count = 1;
long tb = b; // 在后面的代码中不更新b
while((tb+tb)<=a){
count = count + count; // 最小解翻倍
tb = tb+tb; // 当前测试的值也翻倍
}
return count + div(a-tb,b);
}
};
34. 在排序数组中查找元素的第一个和最后一个位置 ⭐⭐
审题
- 升序排列的数组,有重复数字,数字可为负数
- 找的数不存在,返回[-1,-1]
- 思路:
- 直接:
- 迭代
- 进阶:
- 二分查找:问题,如何找到起始的点?
- 直接:
1. 顺序遍历
时间复杂度O(n),没有充分利用到升序数组这个条件
public int[] searchRange(int[] nums, int target) {
int start = -1;
int end = -1;
int[] res = new int[2];
for(int i = 0; i < nums.length; i++) {
if(target < nums[i]) {
break;
}
if(target == nums[i] && start == -1) {
start = i;
end = i;
}else if(target == nums[i]) {
end++;
}
}
res[0] = start;
res[1] = end;
return res;
}
2. 二分查找
不仅对整体二分查找,还二分查找中点target的左右端点。
public int[] searchRange(int[] nums, int target) {
int[] res = new int[]{-1,-1};
int f1 = binarySearch(nums,0,nums.length - 1,target);
if(f1 != -1) {
int left = f1;
int right = f1;
while(true) {
// 临时保存binarSearch结果,避免重复运算
int l_temp;
int r_temp;
if(left == -1 && right == -1) {
break;
}
if(left != -1) {
l_temp = binarySearch(nums,0,left - 1,target);
if(l_temp == -1) {
res[0] = left;
}
left = l_temp;
}
if(right != -1) {
r_temp = binarySearch(nums,right + 1,nums.length - 1,target);
if(r_temp == -1) {
res[1] = right;
}
right = r_temp;
}
}
}
return res;
}
// 二分查找
public int binarySearch(int[] nums, int l, int r,int t) {
while(l < r) {
int m = (l + r) / 2; // 靠左边
// 注意这里+1 和 -1,必要的
if(nums[m] < t) {
l = m+1;
}else if(nums[m] > t) {
r = m-1;
}else{
return m;
}
}
// 如果l==r还要判断中间值
if(l == r) {
if(nums[r] == t)
return r;
}
return -1;
}
**补充:**官方题解的方法是设置bool值来表明是查找第一个大于target和第一个大于等于target的值
反思
- 二分法想起容易,写起来还是十分费劲,自己写有很多的bug
36. 有效的数独 ⭐⭐
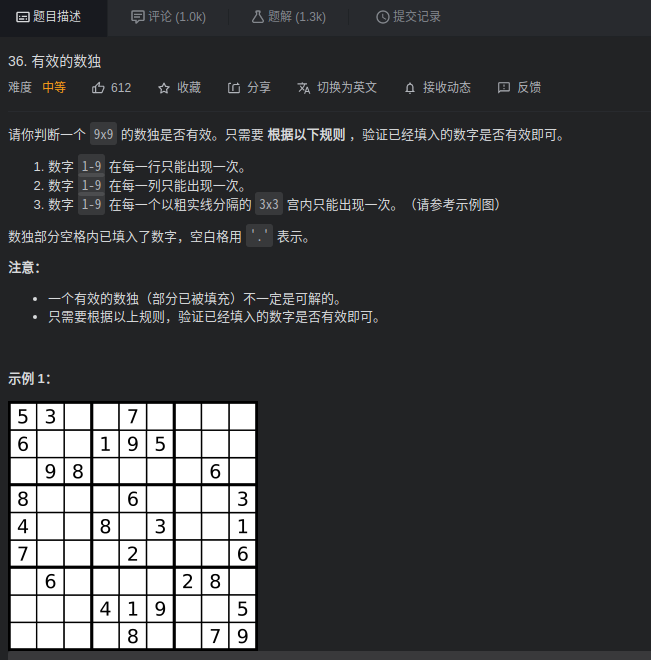
审题
- 分区域 ,每行每列每九宫格
........已经不知道自己有多蠢了,题的意思是求出题中所给缺陷数独是否符合规范!!而不是求是否能生成一个数独。。。搁这做了半天一直不对。。。
看题!!!看题!!!看题!!!
最后摘一道题解,日后再做一下
1. 顺序检验(转)
bool isValidSudoku(vector<vector<char>>& board) {
int row[9][10] = {0};// 哈希表存储每一行的每个数是否出现过,默认初始情况下,每一行每一个数都没有出现过
// 整个board有9行,第二维的维数10是为了让下标有9,和数独中的数字9对应。
int col[9][10] = {0};// 存储每一列的每个数是否出现过,默认初始情况下,每一列的每一个数都没有出现过
int box[9][10] = {0};// 存储每一个box的每个数是否出现过,默认初始情况下,在每个box中,每个数都没有出现过。整个board有9个box。
for(int i=0; i<9; i++){
for(int j = 0; j<9; j++){
// 遍历到第i行第j列的那个数,我们要判断这个数在其所在的行有没有出现过,
// 同时判断这个数在其所在的列有没有出现过
// 同时判断这个数在其所在的box中有没有出现过
if(board[i][j] == '.') continue;
int curNumber = board[i][j]-'0';
if(row[i][curNumber]) return false;
if(col[j][curNumber]) return false;
if(box[j/3 + (i/3)*3][curNumber]) return false;
row[i][curNumber] = 1;// 之前都没出现过,现在出现了,就给它置为1,下次再遇见就能够直接返回false了。
col[j][curNumber] = 1;
box[j/3 + (i/3)*3][curNumber] = 1;
}
}
return true;
}
除此之外还可以考虑位运算的方法,这里的理解也比较巧妙
38. 外观数列 ⭐
* String 与 StringBuilder 关于效率和递归的使用

1. 递归
/**
* 思路: 这种问题看起来很没有思路但是实际上又和前一项有联系
* 考虑到追根溯源 --- 从尾部解决 然后对每一层进行分析
*/
//String的增删效率低 但是这里我的效率依然很低....
public static String countAndSay(int n) {
if(n==1) return "1";
StringBuilder str=new StringBuilder("");
String bcstr=countAndSay(n-1);
for(int i=0;i<bcstr.length();i++){
int j=1;
for(int k=i;k<bcstr.length()-1;k++){
if(bcstr.charAt(i)==bcstr.charAt(k+1)) {
j++;
i++;
}
else break;
}
str.append(String.valueOf(j)+bcstr.charAt(i));
}
return String.valueOf(str);
}
这种做法能做出来,但我觉得基于迭代的 空间复杂度 还有String自身的增添麻烦,且每一次迭代都会新建StringBuilder对象,是会效率不高。
2. 看题解后的细节调整
细节分析: 这里的主要效率不高的拖延点在于str.append 的操作
可能是由于 str.append(String.valueOf(j)+bcstr.charAt(i)); 使得两个字符串再次相加得到的新字符串,再将新的字符串赋值上去,使得在这里出现的String类型的增删。 且append(int ) 添加的是String类型的数字,但由于append(int+char)型的是会先将char 转换成加上int的char 再赋值给builder, 所以这里连用append 更好。
str.append(j).append(bcstr.charAt(i));

42. 接雨水 ⭐⭐⭐

审题
- 区间和高度决定了能够接多少水,以接近区间的最高点和起点决定?
- 算每一个可接单元的每一层吗?
- 做法:先在LogN的时间点找到每个区间,然后在区间内进行运算
- 做后思考:如何在On的情况下计算?
1. 暴力--顺序搜索
以起始点大小为判断条件,找到末点大于起始点的点,分情况讨论:
- 如果找到了 ,则在此基础上以较小的起始点为顶,起始点 - 各点的值逐渐累加
- 没有找到,则找第二大的点,并以末点为顶......
public int trap(int[] height) {
int total = 0;
for(int i = 0; i < height.length; i++) {
for(int j = i+1; j < height.length ; j++) {
// confirm a region
if(height[j] >= height[i]) {
for(int k = i+1; k < j; k ++){
total += height[i] - height[k];
}
i = j - 1;
break;
}
// if can`t find a number bigger than height[i]
if(j == height.length - 1 && height[j] < height[i]) {
int temp = i + 1;
for(j = i + 1; j < height.length; j++) {
if(height[temp] < height[j])
temp = j;
}
j = temp;
for(int k = i+1; k < j; k++) {
total += height[j] - height[k];
}
i = j - 1;
break;
}
}
}
return total;
}
为什么这么慢?
考虑到内部其实有三层循环(但实际上只有两层),最坏时可能对每一个起点,都没有一个比他大的点,并且第二大的点都在末尾排列,所以时间复杂度来到了O(n^2)
如何消除平方的时间复杂度关键要么换算法类型要么就解决如何找第二大的点
2. 动态编程 (转 - 验)
确实,这个题符合动态编程的特点。要想知道该点处的积水量,即找到该点左右两侧最大值中较小的那个,这里用On的空间复杂度去保存这些点,以便能实现O1的计算,所以能在On的时间复杂度内完成。
public int trap(int[] height) {
int total = 0;
int[] right_max = new int[height.length];
int[] left_max = new int[height.length];
right_max[height.length - 1] = height[height.length - 1];
left_max[0] = height[0];
for(int i = 1; i < height.length; i++) {
left_max[i] = Math.max(left_max[i - 1], height[i]);
right_max[height.length - 1 - i] = Math.max(height[height.length - 1 - i], right_max[height.length - i]);
}
for(int i = 1; i < height.length; i++) {
total += Math.min(left_max[i], right_max[i]) - height[i];
}
return total;
}
3. 栈存储 (转 - 验)
思路与 1 一致,有点像1、2的结合,不需要先遍历,有补偿机制。On的时间复杂度和空间复杂度。但不知道为啥这么慢
int total = 0;
Deque<Integer> stack = new LinkedList<>();
int index = 0;
int distance, rel_height;
while(index < height.length) {
while(!stack.isEmpty() && height[index] > height[stack.peek()]) {
int pop = stack.pop();
if(stack.isEmpty())
break;
distance = index - stack.peek() - 1;
rel_height = Math.min(height[index], height[stack.peek()]) - height[pop];
total += rel_height * distance;
}
stack.push(index++);
}
return total;
4. 超妙双指针 (转)
On的时间复杂度 O1的空间复杂度 。非常的妙,以相向的双指针处的值的当前差值来决定从哪边进行补偿,并存储了对应两边的最大值。而又由于其双指针差值选择避开了出现较小的值导致错误补偿的可能
public int trap(int[] height) {
int left = 0, right = height.length - 1;
int ans = 0;
int left_max = 0, right_max = 0;
while (left < right) {
if (height[left] < height[right]) {
if (height[left] >= left_max) {
left_max = height[left];
} else {
ans += (left_max - height[left]);
}
++left;
} else {
if (height[right] >= right_max) {
right_max = height[right];
} else {
ans += (right_max - height[right]);
}
--right;
}
}
return ans;
}
// 链接:https://leetcode-cn.com/problems/trapping-rain-water/solution/jie-yu-shui-by-leetcode/
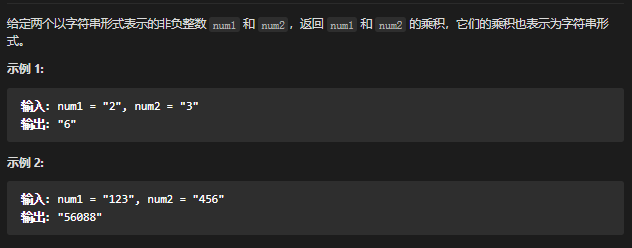
43. 字符串相乘
思考:
不能用Bigdemical 大数相乘 注意最高位数 返回类型为String long可能有溢出
位运算?
1. My 自实现的进位机制
if(num1.equals("0")||num2.equals("0")){
return "0";
}
int l1 = num1.length();
int l2 = num2.length();
int l3 = l1 + l2;
char[] result = new char[l3];
for(int i =0 ;i<l3;i++){
result[i] = '0';
}
//冗杂
int min = Math.min(l1,l2);
if(l1 == min){
String temp =num1;
num1 = num2;
num2 = temp;
}
//选出最小的数
for(int i = num2.length()-1;i>=0;i--){
for(int j = num1.length()-1; j>=0;j--){
int mr = (num1.charAt(j)-48)*(num2.charAt(i)-48);
result[i+j+1] += ( char )(mr % 10 ) ;
if(result[i+j+1] >= 58){
result[i+j] += 1;
result[i+j+1] = (char) (result[i+j+1]-10);
}
//这里有冗杂的成分
result[i+j] += mr/10;
if(result[i+j]>=58){
result[i+j-1] += 1;
result[i+j] -= 10;
}
}
}
if(result[0] == '0'){
return new String(result).substring(1);
}else{
return new String(result);
}
时间复杂度 O(m * n ) 空间复杂度 O(m+n)

整解的思路差不多,但是在处理result[i+j-1]这一块更加简洁
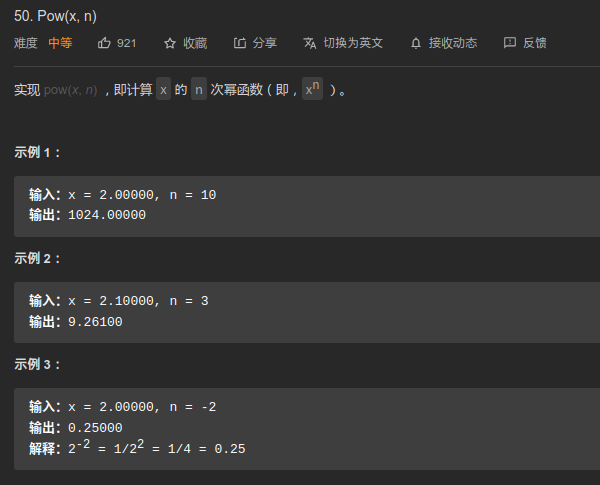
50. Pow(x,n) ⭐⭐
Time : 2022 / 4 / 5 10 : 46
TAG : Iteration / Recursion / Complement / Bits
审题
- x是小数,返回的也是double类型数字.指数可能为负数
- 可能的做法:
- 思路:
- 简单:递归;递归
- 进阶:能否在对数时间复杂度内完成
1. 递归(Stack Over)
public double myPow(double x, int n) {
if(n > 0) {
return myPow(x,n-1)*x;
}
if(n == 0) {
return 1.0;
}
return myPow(1/x,-n);
}
优化(Stack OF)
public double myPow(double x, int n) {
return myPow(x,(long)n);
}
public double myPow(double x, long n) {
if(n == 0) {
return 1.0;
}
if(n < 0) {
return myPow(1/x,-n);
}
if(n / 3 > 0) {
return myPow(x * x * x , n / 3) * myPow(x,n % 3);
}
if(n / 2 > 0) {
return myPow(x * x,n / 2) * ((n & 1) == 1?x:1);
}
return x;
}
2. 迭代(OverTime)
public double myPow(double x, int n) {
if(n == 0) {
return 1.0D;
}
if(n < 0) {
n = -n;
x = 1/x;
}
double res = x;
while(--n > 0) {
res = res * x;
}
return res;
}
优化
public double myPow(double x, int n) {
if(n == 0) {
return 1.0D;
}
Long longx = new Long(n);
if(n < 0) {
longx = Math.abs(longx);
x = 1/x;
}
if(longx == 1) {
return x;
}
double res = 1.0d;
while(longx / 2> 0) {
res = res * ((longx & 1) == 0?1.0:x);
x = x * x ;
longx /= 2;
}
res *= x;
return res;
}
问题
这里还涉及到了自己的一个学习漏洞,对补码的理解和计算机位表示的混乱理解:
具体解析参见文章《计算机组成原理》 [补码的加减法]章节
这道题我的问题主要在于:signed int (1 >> 31 - 1)等于多少,这里应该从位的角度先去理解,计算-1的补码然后二者相加,因为是补码运算,所以符号位囊括在计算过程中。(而-a = ~a+1,这一点也很重要,简化理解过程),得到二进制存储后,再根据对应的数据类型去转化,这里得到的其实是1>>31,而又是signed int,所以结果又根据原码->补码的反操作来求补码->原码,得到原码的值应该是-1>>31。
总结一下就是:完全按照计算机的步骤来,不要自己一会补码运算一会原码相加,把自己都搞混了
总结
一直想做这道题,今天终于还是抽时间写了这道题。这道题踩到坑了,最开始用迭代和递归,都没做出来,要么超时要么StackOF。以为是算法本身的问题,但后来实在没办法,想了想后觉得奇怪。一调试发现一个重要的问题!也是非常基础的问题(只怪自己基础不牢固)
53. 最大子序和 ⭐⭐

思考
O n 的解法
动态规划?
1. My DP
public int maxSubArray(int[] nums) {
int max = nums[0];
int[] dp = new int[nums.length];
dp[0] = nums[0];
for(int i =1;i<dp.length;i++){
dp[i] =Math.max(dp[i-1]+nums[i],nums[i]);
max = Math.max(dp[i],max);
}
return max;
}
dp 序列求,最开始题没看清楚以为求的是数组子序列, 设置了end 和begin,后来一看只求最大值 ...
空间复杂度 On 时间复杂度 On

改进
动态规划需要额外的数组一般是可以改进的
所以这里我改进了之后
public int maxSubArray(int[] nums) {
int max = nums[0];
int dp_pre = nums[0];
for(int i =1;i<nums.length;i++){
dp_pre =Math.max(dp_pre+nums[i],nums[i]);
max = Math.max(dp_pre,max);
}
return max;
}
空间复杂度变为O 1

2. 分治 线段树
....

再回首
1. 动态规划
既然要找出数组最大和的连续子数组,那可以这样想,从1开始,在整个数组中找出以第i个数结尾且和最大的子数组。为什么这样?这样就有递推式:
- 以当前元素结尾且包含前一个元素
- 以当前元素结尾但不包含前一个元素
则有表达式
class Solution {
public int maxSubArray(int[] nums) {
int[] sumsArr = new int[nums.length];
int curMaxSum = nums[0];
sumsArr[0] = nums[0];
for(int i = 1; i < nums.length; i++) {
sumsArr[i] = Math.max(sumsArr[i - 1] + nums[i], nums[i]);
curMaxSum = Math.max(sumsArr[i], curMaxSum);
}
return curMaxSum;
}
}
最终再将maxSubArrSums优化,转化成一个变量即可
2. 分治(线段树) (R)
求一个数组的最大连续子序列和,那可以分成左右两部分来看:
这样就已经解决了两种情况了,只需要解决最后一种左右部分交集的子段和,如何处理?这就引申出来了一个整体的从左开始的最大子段和和从右结束的最大子段和,这样
class Solution {
public class Status{
int lSum, rSum, iSum, mSum ;
public Status(int lSum, int rSum, int iSum, int mSum) {
this.lSum = lSum;
this.rSum = rSum;
// 区间和
this.iSum = iSum;
// 最大子段和
this.mSum = mSum;
}
}
public int maxSubArray(int[] nums) {
return getStatus(nums, 0 , nums.length - 1).mSum;
}
public Status getStatus(int[] nums, int l, int r) {
if(l == r) {
return new Status(nums[l],nums[l], nums[l], nums[l]);
}
int m = (l + r) >> 1;
Status left = getStatus(nums, l, m);
Status right = getStatus(nums, m + 1, r);
return sumLeftAndRightSub(left, right);
}
public Status sumLeftAndRightSub(Status left, Status right) {
int iSum = left.iSum + right.iSum;
int lSum = Math.max(left.lSum, left.iSum + right.lSum);
int rSum = Math.max(right.rSum, right.iSum + left.rSum);
int mSum = Math.max(Math.max(left.mSum, right.mSum), left.rSum + right.lSum);
return new Status(lSum, rSum, iSum, mSum);
}
}
时间复杂度:O(n)(分治是O(logN), 但是遍历了所有节点) 空间复杂度:(OlogN)
这种方法还要维护额外的变量,有递归的调用,有什么好处呢?关键是它是一种类似线段树的想法,可以解决任何子区间[l, r]之间问题,在建成树状结构后,只需要O(logN)的时间复杂度就可以求出答案
55. 跳跃游戏 ⭐⭐
审题
- 非负整数数组,代表最大可跳步数,判断的是能否跳到最后一个下标
- 可能的算法:DFS / dp
- 可以做一些优化,比如元素值都大于0,则true
- 思路:
- 简单:
- DFS:构建回溯方法,当前索引,当前所跳步数
- 进阶:一次遍历后是否可行?按理说可以
- DP:
- 简单:
1. DFS(OverTime)
超时,但结果应该是对的。IDEA上测1000次超时数组,此方法用时14ms,dp用时3ms,超时没问题
三次搜索,三种情况的并集(需要考虑判断正负的条件):
- 当前最大步数下的下一个索引位置
- 邻接的下一个索引开始
- 当前步数-1搜索
class Solution
public boolean canJump(int[] nums) {
boolean res = false;
boolean allPositive = true;
for(int i = 0; i < nums.length; i++) {
if(nums[i] <= 0)
allPositive = false;
}
if(allPositive) {
return true;
}
res = dfs(nums,0,nums[0]);
return res ;
}
private boolean dfs(int[] nums, int index, int cur_step) {
if(index >= nums.length || (cur_step == 0 && index != nums.length - 1)) {
return false;
}
if(nums[index] + index == nums.length - 1 || (index == nums.length - 1)) {
return true;
}
boolean longJmp = false;
boolean nextJmp = false;
boolean decreaseJmp = false;
if(cur_step + index < nums.length) {
longJmp = dfs(nums,index + cur_step, nums[index +cur_step]);
}
if(index + 1 < nums.length) {
nextJmp = dfs(nums,index+1, nums[index+1]);
}
decreaseJmp = dfs(nums,index, cur_step - 1);
return longJmp | nextJmp | decreaseJmp ;
}
}
2. DP / 贪心
DP ! 我滴超人!(其实是贪心hhh)
激动的心,颤抖的手,这道题的答案我KO
当然理论还是因为两点:
- 可以通过一次遍历得到
- 当前boolean值可以由上一个元素的是否可行的boolean值推出
DP的推导:
dp中记录的是到了当前这一个索引,还剩下多少步数(也就是最大步数,所以是贪心)可以走(因为步数肯定是连续的,从0 - m)
- dp[i - 1] <= 0不能够到达dp[i]
- dp[i - 1] > 0 能到达,这时要考虑dp[i]的值的取舍,因为保持的是当前索引还剩下的最大步数,为确保最大,则需要在nums[i]和dp[i - 1] - 1上做出取舍,取最大值。
class Solution {
public boolean canJump(int[] nums) {
boolean res = false;
boolean allPositive = true;
if(nums.length == 1) {
return true;
}
// 优化一,一次遍历 能确定true但不能确定false
for(int i = 0; i < nums.length; i++) {
if(nums[i] <= 0)
allPositive = false;
}
if(allPositive) {
return true;
}
// 可优化点三,dp[] -> dp (int)
int[] dp = new int[nums.length];
dp[0] = nums[0];
for(int i = 1; i < nums.length; i++) {
// 优化二,可直接调到最后一个,就可以直接判断正
if(dp[i - 1] + i - 1 >= nums.length -1) {
return true;
}
if(dp[i - 1] <= 0) {
dp[i] = 0;
return false;
}else{
dp[i] = Math.max(dp[i - 1] - 1, nums[i]);
}
}
return dp[nums.length - 1] >= 0;
}
}
这个结果我非常满意哈哈哈
优化的重要性
可能是题库给的测试数据偏向问题,这里我去掉了前面的一次遍历(判断是否都为正数的情况,因为全部为正数则肯定可以通过)。结果相当哇塞
没想到去掉了原以为影响不大的一次遍历,O(n)上不会有影响,但实际却还是相差甚远,优化的重要性是不言而喻的.这里之后应该是某几次偏差,删除后又试了下,恢复正常94%,因为题解方法最慢都是O(n),只是操作上多做了几步判断,这里这样做其实意义不是很大。
还有一个优化就是可直接一步跳到最后一格,则判正(不过貌似加上影响不大,还与添加位置有关系)
dp最根本的优化
忘记了dp最根本的优化思路,即把数组替换成单个变量!
3. 简洁的思路(转)
表示当前索引下还可以跳多远,思路相似
public static boolean canJump(int[] nums) {
if (nums == null) {
return false;
}
//前n-1个元素能够跳到的最远距离
int k = 0;
for (int i = 0; i <= k; i++) {
//第i个元素能够跳到的最远距离
int temp = i + nums[i];
//更新最远距离
k = Math.max(k, temp);
//如果最远距离已经大于或等于最后一个元素的下标,则说明能跳过去,退出. 减少循环
if (k >= nums.length - 1) {
return true;
}
}
//最远距离k不再改变,且没有到末尾元素
return false;
}
反思
- On 一次遍历的思路帮大忙,优化的思路还是不错
- dp最终优化没有想到,化数组为单变量
- DFS不是很熟悉,好在磨了一会后想到了
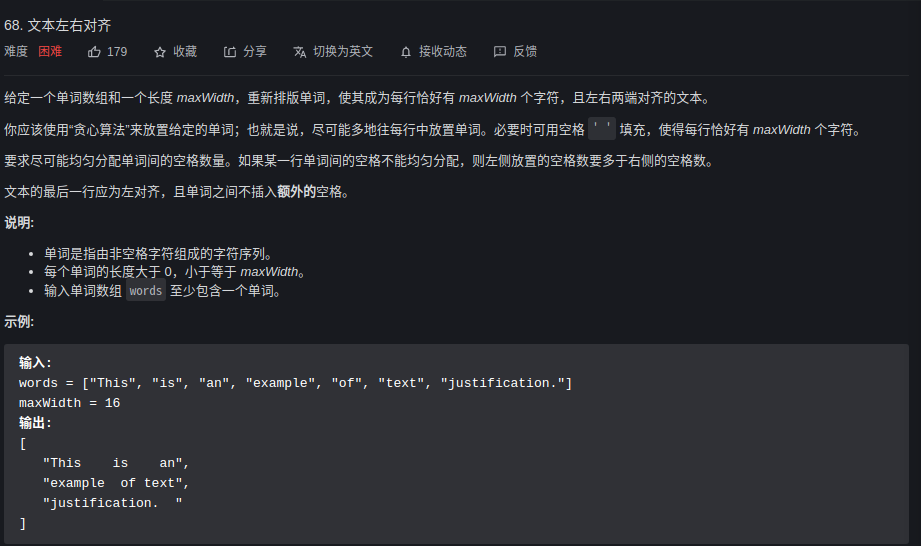
68. 文本左右对其 ⭐⭐⭐
审题
每行至少有一个word
要求尽可能均匀分配单词间的空格数量。如果某一行单词间的空格不能均匀分配,则左侧放置的空格数要多于右侧的空格数。
文本的最后一行应为左对齐,且单词之间不插入额外的空格。
空格情况: 均分、不均分
1. 核心步骤拆分法硬解...
直接硬解,核心部分拆分成两个方法
- 一行中多少个单词
- 一行中的单词如何排列
- 均分
- 不均分情况
- 最后一排
- 只有一个单词情况
public List<String> fullJustify(String[] words, int maxWidth) {
List<String> result = new ArrayList<>();
// detect how many numbers it can contain
int column = 0;
int index = 0;
String newLine;
while(index < words.length){
int size = getMaxNumInSingle(words,maxWidth,index);
String single = makeSingleStr(words,maxWidth,index,size);
result.add(single);
index+=size;
}
return result;
}
// 获取单行有多少个字母
public int getMaxNumInSingle(String[] words, int maxWidth, int index) {
int length = 0;
int size = 0 ;
for(;index<words.length;index++) {
if(length + words[index].length() == maxWidth) {
size ++;
break;
}
if(length + words[index].length() > maxWidth) {
break;
}
if(length + words[index].length() < maxWidth) {
// 加1 是因为空格,这里下加上不加很重要
length += words[index].length() + 1;
size ++;
}
}
return size;
}
// 获取单行单词排列后String StringBuilder此处可优化
public String makeSingleStr(String[] words, int maxWidth, int index, int size) {
int i = index;
int allLength = 0;
StringBuilder str = new StringBuilder();
// 一个单词情况
if(size == 1){
str.append(words[index]);
for(int j = 0; j<maxWidth-words[index].length();j++){
str.append(" ");
}
return str.toString();
}
// 最后一行情况
if(index+size == words.length) {
for(int k = index; k<index+size-1; k++) {
str.append(words[k]);
str.append(" ");
}
str.append(words[index+size-1]);
int strLength = str.length();
for(int k = 0; k<maxWidth-strLength;k++){
str.append(" ");
}
return str.toString();
}
while(i<index+size) {
allLength += words[i].length();
i++;
}
int curSpaces = 0;
for(int k = index; k < index+size-1; k++ ){
str.append(words[k]);
int temp = curSpaces;
if(((maxWidth - allLength - temp)% (index+size-k-1)) == 0 ){
for ( int j = 0 ;j<(maxWidth - allLength - temp)/(index+size-k-1);j++) {
str.append(" ");
curSpaces ++;
}
}
else {
for ( int j = 0 ;j<(maxWidth - allLength - temp)/(index+size-k-1)+1;j++) {
str.append(" ");
curSpaces++;
}
}
}
str.append(words[index+size-1]);
return str.toString();
}
这道题做起来真的还是很慢,1h......前前后后太多小错误没有顾忌到,另外String的长度是length()而不是length...
StringBuilder处可优化
也提供了一种解题思路吧,以后面对这种步骤性强的题,自己可以分成几步,然后分步解决,思路会清晰很多。
看了题解的方法,通过模拟,列举出各种情况,对这些情况一一讨论,和我这里的思路比较相似,不过在处理多个单词上,他的做法更好
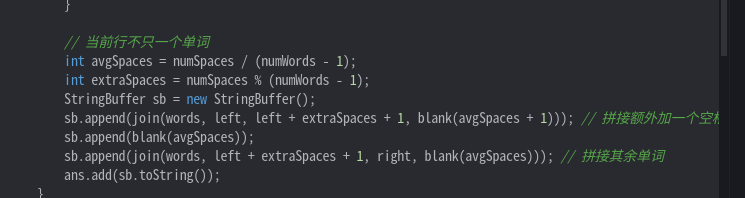
这里学习一下这种方法...
69. x 的平方根 ⭐
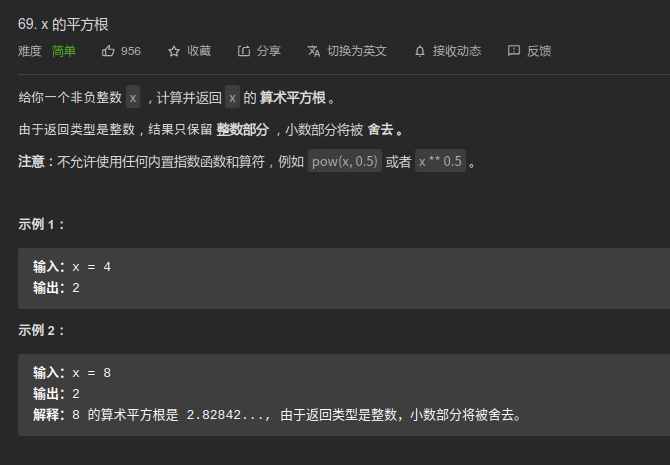
牛顿迭代法:
static int sqrtByNewton(int x){
long i=x;
while((long)i*i>x){
i=(i+x/i)/2;
}
return (int)i;
}

二分法:
static int sqrtWithBinary(int x){
long result=-1;
long left=0,right=x/2+1,mid;
while(true){
mid=(right+left+1)/2;
if(mid*mid>x){
right=mid-1;
}else if(mid*mid<x){
left=mid;
result=mid;
}else{
return (int)mid;
}
if(left>=right)
return (int)right;
}
/*
分析: 此处mid=(right+left+1)/2; 必须是在右中部。因为在左中部容易出现无限循环的现象
*/
}

用除法避免 int 溢出的情况
用 int 型测试较大数字时, 由于 i*i 可能溢出,所以 需要提前设置为long 型 ,而后强转为 int
public int mySqrt(int x) {
if(x==1||x==0)return x;
int left=0,right=x/2+1;
while(left<right){
int mid=left+(right-left)/2;
if(x/mid==mid||(x/mid>mid&&x/(mid+1)<(mid+1))){//刚好
return mid;
}
else if(x/mid>mid){//mid比根小
left=mid;
}
else{//mid比根大
right=mid;
}
}
return -1;
}
75. 颜色分类 ⭐⭐

审题
- 原地排序,返回的还是原来的数组
- 想法:三指针标识当前位置.难点:前段的插入会导致后一段向后移动。想法变更:先统计次数,然后提前设置好分界点
1. 顺序移位(X)
public static void sortColors(int[] nums) {
int[] color = new int[3];
int i = 0;
int temp = nums[0];
for(; i < nums.length; i++) {
color[nums[i]]++;
}
i = 0;
int[] cntColor = new int[3];
while(i < nums.length) {
temp = nums[i];
if(cntColor[nums[i]] == color[nums[i]]) {
i++;
continue;
}
int min,max,k;
min = max = 0;
for(k = 0; k < nums[i]; k++) {
min += color[nums[i]];
}
max = min + color[k];
if(i < max && i >= min) {
i++;
continue;
}
int total = 0;
for(int z = 0; z < nums[i]; z++) {
total += color[z];
}
nums[i] = nums[cntColor[nums[i]] + total];
nums[cntColor[temp] + total] = temp;
cntColor[temp]++;
if(i >= max || i < min){
continue;
}
i++;
}
通过用例 85/87.......
基于三指针
2. 单指针--多趟(R)
利用单指针,先一遍将0排好,再将1排好,在LogN的时间复杂度内解决问题。要注意ptr究竟代表了什么 ---> 当前最小数字的最远索引
不要小瞧这种在LogN的复杂度内多次遍历的情况,因为最终也代表了LogN的复杂度
3. 双指针(R)
针对0 和 1的顺序双指针
注意:搞清楚P1 和 P2到底指向什么---> 开始处那么我们可能会把一个 1 交换出去。当 p_0 < p_1时,我们已经将一些 1连续地放在头部,此时一定会把一个 1交换出去,导致答案错误
4. 双指针(R)
针对0 和 2 的相向双指针
相比之前的做法,也有需要注意的点:即2的指针交换i处位置后,要考虑交换的是什么,不能交换完就进行下一处交换了,因为可能交换后nums[i]的值是0或2.所以需要不停交换,直至不为2.
104. 二叉树的最大深度 ⭐
我的代码:
递归法
public int maxDepth(TreeNode root) {
int left=0,right=0;
/*
try catch 抓nullpointer异常,避免报错
*/
try{
if(root.left==null&&root.right==null){
return 1;
}
left= 1+maxDepth(root.left);
right= 1+maxDepth(root.right);
}
}catch(NullPointerException e){
}
return left>right?left:right;
}

思考
判断 Null 型对象以后 还是加上try -catch 语句更好
学会使用
left= 1+maxDepth(root.left); right= 1+maxDepth(root.right);类的递归方法
105. 前中序构造二叉树 ⭐⭐
思路
递归 node.left = .....
1. My 递归
public TreeNode buildTree(int[] preorder, int[] inorder) {
return addLR(0,preorder.length-1,new TreeNode(),preorder,inorder,0);
}
public TreeNode addLR(int l,int r,TreeNode node,int[] preorder, int[] inorder,int i){
if(l>r){
return null;
}
if(l==r){
return new TreeNode(inorder[l]);
}
int index = lookForPre(preorder[i],inorder);
if(node == null)
node = new TreeNode();
node.val = inorder[index];
node.left = addLR(l,index-1,node.left,preorder,inorder,i+1);
node.right = addLR(index+1,r,node.right,preorder,inorder,i+index-l+1);
return node;
}
public int lookForPre(int num, int[] inorder){
int j;
for(j =0;j<inorder.length;j++){
if(num == inorder[j])
return j;
}
return -1;
}

时间复杂度 On? 空间复杂度 On
2. hashmap的小改进
public HashMap<Integer,Integer> hashMap;
public TreeNode buildTree(int[] preorder, int[] inorder) {
hashMap = new HashMap();
for(int i =0;i<preorder.length;i++){
hashMap.put(inorder[i],i);
}
return addLR(0,preorder.length-1,new TreeNode(),preorder,inorder,0);
}
public TreeNode addLR(int l,int r,TreeNode node,int[] preorder, int[] inorder,int i){
if(l>r){
return null;
}
if(l==r){
return new TreeNode(inorder[l]);
}
int index = lookForPre(preorder[i]);
if(node == null)
node = new TreeNode();
node.val = inorder[index];
node.left = addLR(l,index-1,node.left,preorder,inorder,i+1);
node.right = addLR(index+1,r,node.right,preorder,inorder,i+index-l+1);
return node;
}
public int lookForPre(int num){
return hashMap.get(num);
}
hashmap增加了On的占用空间但在get num在中序数组中的位置时非常快....
看来hashmap在算法题中还是很重要,设计到for循环查找时还是要考虑一下
3. 迭代 + 栈
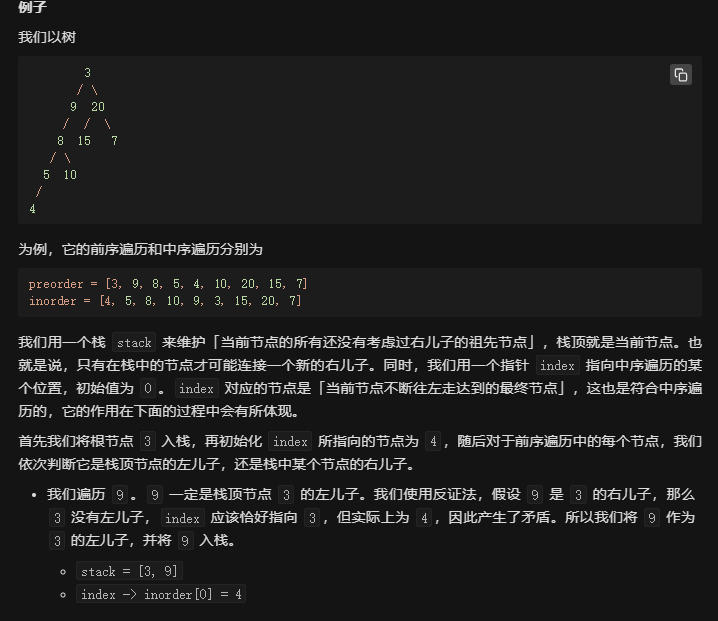
也是类似阿里栈算法的那道题,比较难想.....
112. 路径总和⭐
1. 递归(R)
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if(root == null) {
return false;
}
if(root.left == null && root.right == null) {
return (targetSum - root.val == 0);
}
return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val);
}
}
反思
自己做这种递归题老是容易想多.....
113. 路径总和II⭐⭐
思路
- 输出所有可能的路径;根节点到叶子结点;注意: 不是找到一条合适的路径就可以返回了,这里必须要遍历完所有的路径。
- 直接:遍历所有从根节点到叶子结点的可能,成功则将其加入到List中
1. 遍历/DFS
核心思路还是与LeetCode-112.路径总和的问题差不多,但是需要注意的是这里是需要遍历完所有路径的。采用只能在一端增删的List
- 对当前不为空的元素,先添加进当前List中,递归判断是否是叶子结点且满足targetSum
- 是:拷贝一份当前List副本并且存放至外层List中, 并且将当前元素从队尾删除
- 否:更新当前List的索引(最新元素的位置)。递归计算其左、右孩子是否满足条件。最终将当前元素从队尾删除
需要注意的是,这里递归前后涉及到元素的队尾插入和队尾删除操作,也是有DFS思想的。
class Solution {
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> total = new ArrayList<>();
List<Integer> list = new ArrayList<>();
method(root, targetSum, list, total, 0);
return total;
}
// index: 维护队尾状态的索引指针
public void method(TreeNode root, int targetSum, List<Integer> list, List<List<Integer>> total, int index) {
if(root == null) {
return;
}
if(root.left == null && root.right == null) {
if(targetSum - root.val == 0) {
list.add(root.val);
// add to total list
List<Integer> temp = new ArrayList<>();
for(int i = 0; i < list.size(); i++) {
temp.add(list.get(i));
}
total.add(temp);
list.remove(list.size() - 1);
return;
}
}
list.add(root.val);
int curIndex = list.size() - 1;
method(root.left, targetSum - root.val, list, total, curIndex);
method(root.right, targetSum - root.val, list, total, curIndex);
list.remove(curIndex);
}
}
121. 买卖股票 ⭐
我的代码:
暴力法
//暴力法: for二重循环 两指针索引 遍历 //缺点 : 时间慢, 有重复计算 //时间复杂度: O(n^2) 空间复杂度 O(1)--一个常量 public static int maxProfit(int[] prices) { int max=0; for(int i=0;i<prices.length;i++){ for(int j=prices.length-1;j>i;j--){ if(prices[j]-prices[i]>max) { max = prices[j] - prices[i]; } } } return max; }
image-20201007090734202
动态规划
//动态规划 一次遍历
//原因: 买入的 股票价格总是在最前面!!!
//时间复杂度: O(n) 空间复杂度 O(1)--两个常量
public static int maxProfit_2(int[] prices) {
int max=0,min=Integer.MAX_VALUE;
for(int i=0;i<prices.length;i++){
if(prices[i]<min)
min=prices[i];
else if(prices[i]-min>max) //这一步很重要
max=prices[i]-min;
}
return max;
}
134. 加油站 ⭐⭐
在所求点后的过程量 >= 0 的情况
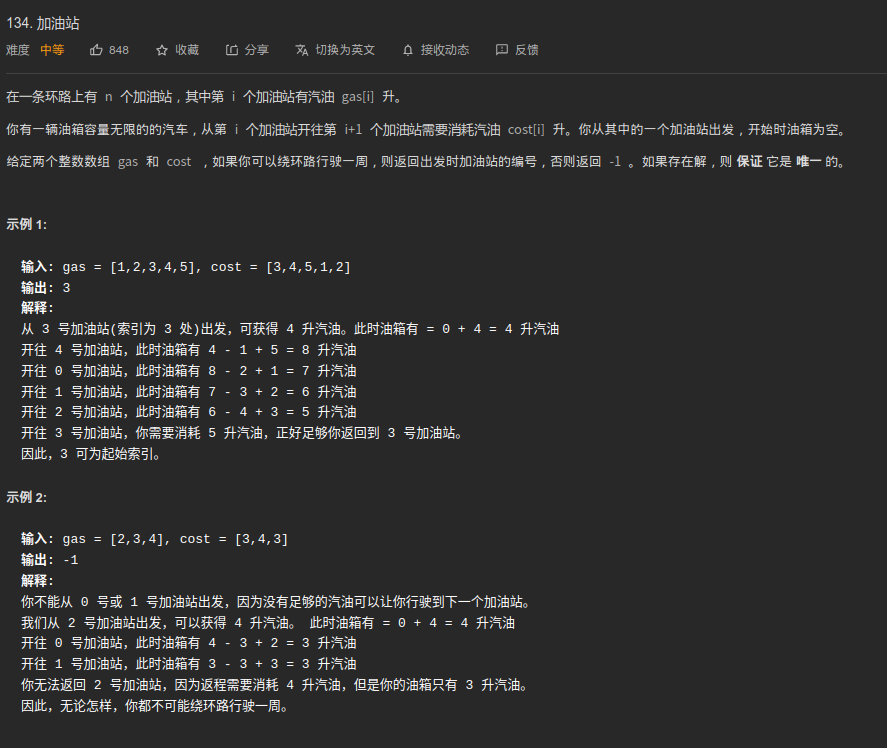
审题
- 油箱容量是无限的,开始油箱为空 ; 若存在解 则解唯一、
- 可能的数据结构:
- 可能的算法:迭代?动态规划?
- 先尝试最简单的:依次循环
1. 暴力迭代
class Solution {
public int canCompleteCircuit(int[] gas, int[] cost) {
int i = 0;
int res ;
for(; i < gas.length; i++) {
res = 0;
for(int j = 0; j < gas.length; j++) {
if(i + j >= gas.length) {
res += gas[i + j - gas.length];
res -= cost[i + j- gas.length];
}else{
res += gas[i + j];
res -= cost[i + j];
}
if(res < 0) {
break;
}
}
if(res >= 0){
return i;
}
}
return -1;
}
}
理所应当的超时.....
稍稍优化:temp[i] = gas[i] - cost[i];
2. 一次遍历
捞汁巨聪明,核心还是两个数组差值组成的新数组到达某一限度的判定问题。核心:
- before:管之前没有达标的那一部分数,就不用之后再回归头算一次了
- res:管当前可能的累计和,有可能不会<0,也可能<0。如果<0,则就需要累加到before上并清零这个res
- 若最终before + res < 0 则不存在这样的点,因为遍历了所有的点都不行
这里我优化了一下:
- 能够到达加油站的必要条件:差值数组和必须大于0
这里单独把差值数组提前算出来是没有意义的,浪费了On的空间,所有结果的空间复杂度这么高,其余的话应该都是最优的。
public int canCompleteCircuit(int[] gas, int[] cost) {
int n = gas.length;
int res;
int before ;
int index = 0;
int[] temp = new int[n];
for(int i = 0; i < n; i++) {
temp[i] = gas[i] - cost[i];
}
int sum = 0;
for(int i = 0; i < n; i++) {
sum += temp[i];
}
if(sum < 0)
return -1;
before = 0;
res = 0;
for(int i = 0; i < n; i++) {
if(temp[i] < 0 && res + temp[i] < 0){
if(res + temp[i] < 0){
before += res + temp[i];
res = 0;
index = i + 1;
}
}else{
res += temp[i];
}
}
if(res + before < 0)
return -1;
return index;
}
解决一个自己很蠢的问题:
数组超出长度后回到头部:(i+cnt)%arr.length....不要再用什么if else判断了
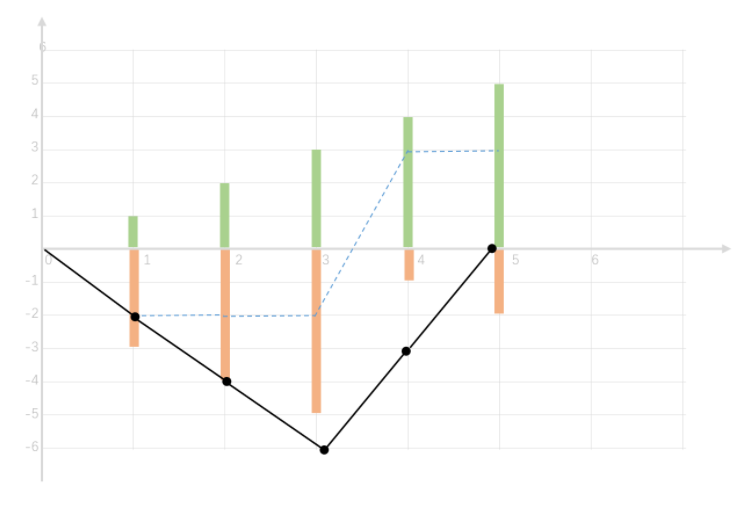
3. 折线图的思想
一种很巧妙的方法,也是不容易想通的。找出差值的最小值点,折线图表示的是以0加油站为起点的(在0加油站时没加油也没耗油)油耗情况,绿色代表gas 黄色代表cost。
折线图表示的肯定是一个或者多个V形的走势,那只需要把最小的那个点找出来,以那个点的下一个站为起点,在最终油量剩余量 >= 0的情况下,肯定过程油量的>=0的(因为图的起点不一样了,以那个站点为起点,则不可能再出现X轴的情况) 可以理解是把图像竖直平移再水平平移(更换了站点)
public int canCompleteCircuit(int[] gas, int[] cost) {
int len = gas.length;
int spare = 0;
int minSpare = Integer.MAX_VALUE;
int minIndex = 0;
for (int i = 0; i < len; i++) {
spare += gas[i] - cost[i];
if (spare < minSpare) {
minSpare = spare;
minIndex = i;
}
}
return spare < 0 ? -1 : (minIndex + 1) % len;
}
// 作者:cyaycz
// 链接:https://leetcode-cn.com/problems/gas-station/solution/shi-yong-tu-de-si-xiang-fen-xi-gai-wen-ti-by-cyayc/。
作者的结果显示内存消耗为 72%,可能有误差,但这确实也从图像的方向上提供了一个非常好的思路
137. 只出现一次的数字II ⭐
只出现一次的数字I -----
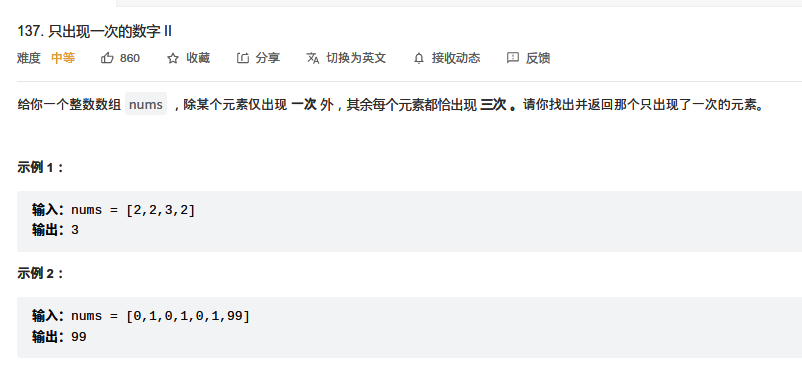
审题
1. Hash + List缓存
这个做法治标不治本,因为他并没有区分是其他数字都重复了三次,如果其他数字重复了N次,也可以通过这个做法来算,所以他不太可能是针对当前算法的最好解法,只能说是通解
public int singleNumber(int[] nums) {
List<Integer> list = new ArrayList<>();
Map<Integer,Integer> map = new HashMap<>();
for(int i = 0; i < nums.length; i++) {
if(map.get(nums[i]) == null) {
map.put(nums[i], 1);
list.add(nums[i]);
}else{
int temp = map.get(nums[i]);
map.put(nums[i],++temp);
}
}
for(int i = 0; i <list.size(); i++) {
if(map.get(list.get(i)) == 1) {
return list.get(i);
}
}
return nums[0];
}
O(2N)的时间复杂度 O(N)的空间复杂度。直接遍历Hash表的键值对也可以,这样空间复杂度能提到70%
2. 有限状态自动机(转)
146. LRU缓存 ⭐⭐
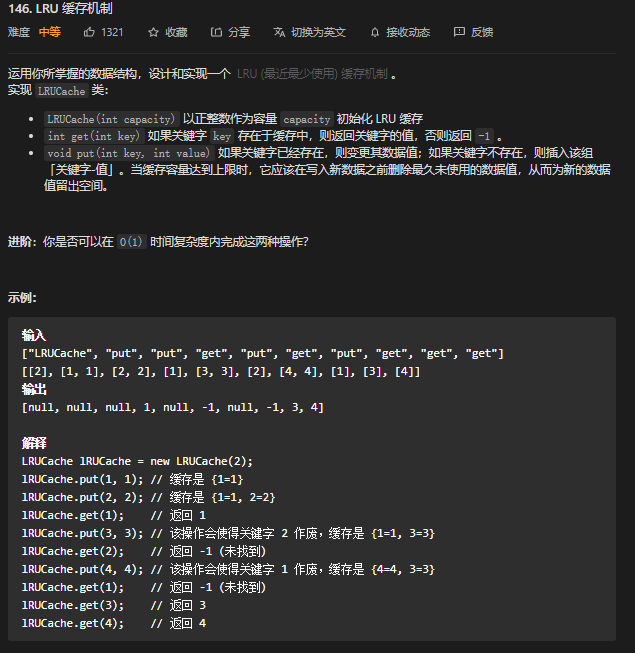
思考
get 和 put的方法说明
1. My LruHashMap
static class Node {
Node next,prev;
int key;
int value;
Node(int key,int value){
this.key = key;
this.value = value;
}
Node(){}
}
private HashMap<Integer,Node> cache;
private int size;
private int MaxSize;
private Node head,tail;
public LRUCache(int capacity) {
cache = new HashMap();
size = 0;
MaxSize = capacity;
head = new Node();
tail = new Node();
tail.prev = head;
head.next = tail;
}
public int get(int key) {
Node res = cache.get(key);
if(res == null) {
return -1;
}
addToTail(res);
return res.value;
}
public void put(int key, int value) {
if(size == 0){
Node node = new Node(key,value);
head = node;
tail = node;
size++;
cache.put(key,node);
}else {
Node temp = cache.get(key);
if (temp != null) {
temp.value = value;
addToTail(temp);
} else {
Node node = new Node(key, value);
cache.put(key, node);
addNewToTaile(node);
size++;
if (size > MaxSize) {
removeEldest();
size--;
}
}
}
}
public void addNewToTaile(Node node) {
node.next = null;
node.prev = null;
node.prev = tail;
tail.next = node;
tail = node;
}
public void addToTail(Node node){
if(head == tail){
return ;
}
else if(node == tail){
return ;
}
else if(node == head){
Node temp;
temp = node.next;
head = temp;
head.prev =null;
}else{
Node prev,next;
prev = node.prev;
next = node.next;
if(prev == null){
tail = node.next;
tail.prev = null;
}else if(next == null){
}else{
node.prev.next = next;
node.next.prev = prev;
}
}
addNewToTaile(node);
}
public void removeEldest(){
Node temp ;
cache.remove(head.key);
temp = head.next;
head = temp;
head.prev = null;
}
static class Node {
Node next,prev;
int key;
int value;
Node(int key,int value){
this.key = key;
this.value = value;
}
Node(){}
}
private HashMap<Integer,Node> cache;
private int size;
private int MaxSize;
private Node head,tail;
public LRUCache(int capacity) {
cache = new HashMap();
size = 0;
MaxSize = capacity;
head = new Node();
tail = new Node();
tail.prev = head;
head.next = tail;
}
public int get(int key) {
Node res = cache.get(key);
if(res == null) {
return -1;
}
addToTail(res);
return res.value;
}
public void put(int key, int value) {
if(size == 0){
Node node = new Node(key,value);
head = node;
tail = node;
size++;
cache.put(key,node);
}else {
Node temp = cache.get(key);
if (temp != null) {
temp.value = value;
addToTail(temp);
} else {
Node node = new Node(key, value);
cache.put(key, node);
addNewToTaile(node);
size++;
if (size > MaxSize) {
removeEldest();
size--;
}
}
}
}
public void addNewToTaile(Node node) {
node.next = null;
node.prev = null;
node.prev = tail;
tail.next = node;
tail = node;
}
public void addToTail(Node node){
if(head == tail){
return ;
}
else if(node == tail){
return ;
}
else if(node == head){
Node temp;
temp = node.next;
head = temp;
head.prev =null;
}else{
Node prev,next;
prev = node.prev;
next = node.next;
if(prev == null){
tail = node.next;
tail.prev = null;
}else if(next == null){
}else{
node.prev.next = next;
node.next.prev = prev;
}
}
addNewToTaile(node);
}
public void removeEldest(){
Node temp ;
cache.remove(head.key);
temp = head.next;
head = temp;
head.prev = null;
}
根据LinkedHashMap 而来 --- 内部节点前后指针,并且存储通过 Key,Node<Key,Value>存
注意特殊情况判断(这里一个bug卡了很久很久),注意插入 时容量判断问题
155. 最小栈 ⭐
思考
1. 自定义
class MinStack {
/** initialize your data structure here. */
class Node{
int val;
Node next;
Node(int val){
this.val = val;
}
}
Node head;
Node min;
public MinStack() {
head = null;
min = head;
}
public void push(int val) {
Node node = new Node(val);
node.next = head;
head = node;
if(min == null){
min = head;
}else if(min.val > val){
min = node;
}
}
public void pop() {
if(head.val == min.val){
Node node = head.next;
min = node;
while(node != null){
min = node.val>min.val ? min:node;
node = node.next;
}
}
head = head.next;
}
public int top() {
return head.val;
}
public int getMin() {
return min.val;
}
}
思路就是维护一个头指针,和一个最小指针,在pop时进行判断,虽然会有偶尔的On时间复杂度,但整体来说是好的。从Lru中学到
162. 寻找峰值 ⭐⭐
审题
- 严格大于
- 包含多个,返回任意一个
- 时间复杂度O(logn),想到了二分?
- 返回的是索引值而不是值
1. 顺序判断
public int findPeakElement(int[] nums) {
if(nums.length == 1){
return 0;
}
if(nums.length == 2) {
return nums[0] > nums[1] ? 0: 1;
}
int index = 1;
while(index < nums.length - 1) {
if(nums[index] > nums[index-1] &&
nums[index] > nums[index + 1]) {
return index;
}
else if (nums[index] < nums[index + 1]){
index++;
}
else {
index += 2;
}
}
if(nums[nums.length - 1] > nums[nums.length - 2]) {
return nums.length - 1;
}
return 0;
}
这里我最开始想到二分查找,但没想到如何二分,index+=2有点二分的意思,但这里不满足Ologn的时间复杂度(例如{1,2,3,4,5,6,7})
2. 二分查找(转)
public int findPeakElement(int[] nums) {
int left = 0, right = nums.length - 1;
for (; left < right; ) {
int mid = left + (right - left) / 2;
if (nums[mid] > nums[mid + 1]) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
目的是:在区间内有峰值
首先要注意题目条件,在题目描述中出现了 nums[-1] = nums[n] = -∞(这是关键!),这就代表着 只要数组中存在一个元素比相邻元素大,那么沿着它一定可以找到一个峰值
感觉还是审题没有仔细。。。
172. 阶乘后的零 ⭐⭐
审题
- 返回的是结果中含有的零的个数(0不算,要尾随)
- 数学层面:
- 2 * 5 = 0
- 思路:
- 直接:算出数,然后依次 / 10 % 10看0的个数。不行:因为实际运算存在溢出
- 进阶:
- 位运算?kcm?dp
- 👍 因式分解 看2 和 5的个数, 因为是尾随所以可以这样做
- 零的个数 = 原本有的 + 进位产生的
- 能否在On 或 Oc的时间复杂度内计算出?
1. 因式分解
我是傻杯之不读题……题的意思是尾随的零的个数,是最后几位全是零的个数,而不是求总的零的个数
故只需要找到 2 和 5的个数即可,取最小值因为除2 * 5外,其他的数相乘都不可能构成尾随零(但有可能构成中间零)
public int trailingZeroes(int n) {
int temp;
int a = 0;
int b = 0;
while(n >= 2) {
temp = n;
while(temp % 5 == 0 && temp /5 != 0) {
temp /= 5;
b++;
}
while(temp % 2 == 0 && temp / 2 != 0) {
temp = temp >> 1;
a++;
}
n--;
}
return Math.min(a,b);
}
时间复杂度在On之上
反向优化
说白了是找5的个数,但是迭代时会有重复的5的倍数的记录,因此之类用map去替代,但效果甚至更差
public int trailingZeroes(int n) {
if(n < 5) {
return 0;
}
int b = 0;
HashMap<Integer,Integer> map = new HashMap<>();
map.put(5,1);
initHashMap(n, map);
for(int i = 5; i <= n; i++) {
b += map.get(i);
}
return b;
}
void initHashMap(int n , Map<Integer,Integer> map) {
int origin;
int temp = 6;
origin = temp;
int lastNum = 1;
while(temp <= n) {
int div = temp / 5;
if(temp % 5 == 0 ) {
if(map.get(div) != null) {
lastNum = map.get(div) + 1;
map.put(temp, lastNum);
}else{
lastNum = 1;
map.put(temp, lastNum);
}
}else{
map.put(temp,0);
}
temp = origin++;
}
}
优化
其实2的个数是远大于5的个数的,所以只用统计5的个数即可
public int trailingZeroes(int n) {
int b = 0;
int temp = n;
while(temp > 4) {
while(temp % 5 == 0 && temp / 5 != 0) {
temp = temp / 5;
b++;
}
temp = --n;
}
return b;
}
2. 数学公式
心态小炸,但还是想出来了
实际上就是数学问题,找n中含有5的个数,然后把这些N加起来,其实可以更宏观的来看,不用从每个数的角度来看。因为本身基于数学,所以肯定是有数学规律的,规律:
每隔5^n - 1个数,就总计会有n个5出现 (思考思路可以从 额外贡献来看)
class Solution {
public int trailingZeroes(int n) {
if(n < 5) {
return 0;
}
int res = 0;
int temp = n;
int par = 5;
while(temp / 5 != 0) {
res += n / par;
par *= 5;
temp /= 5;
}
return res;
}
}
O(log_5{N})的时间复杂度
优化
LeetCode题解,思路相同,但代码简洁许多
public int trailingZeroes(int n) {
int ans = 0;
while (n != 0) {
n /= 5;
ans += n;
}
return ans;
}
反思
- 就估计这道题是数学问题,因为本来最开始使用方法加上优化已经还不错了,但是还是有问题,估计肯定有最简洁的数学公式在Oc的时间复杂度内计算出来
- 应用模型 👉 数学问题的转化还不能很明显的感知(比如这里找2 和 5 然后再到找5的这个过程是不太快速的)
- ⚠️ 看问题有时候太细致,不够宏观,有时候从微观到宏观,从迭代到整体考虑,可能会有新的发现
- 有点死磕.......
189. 轮转数组 ⭐⭐
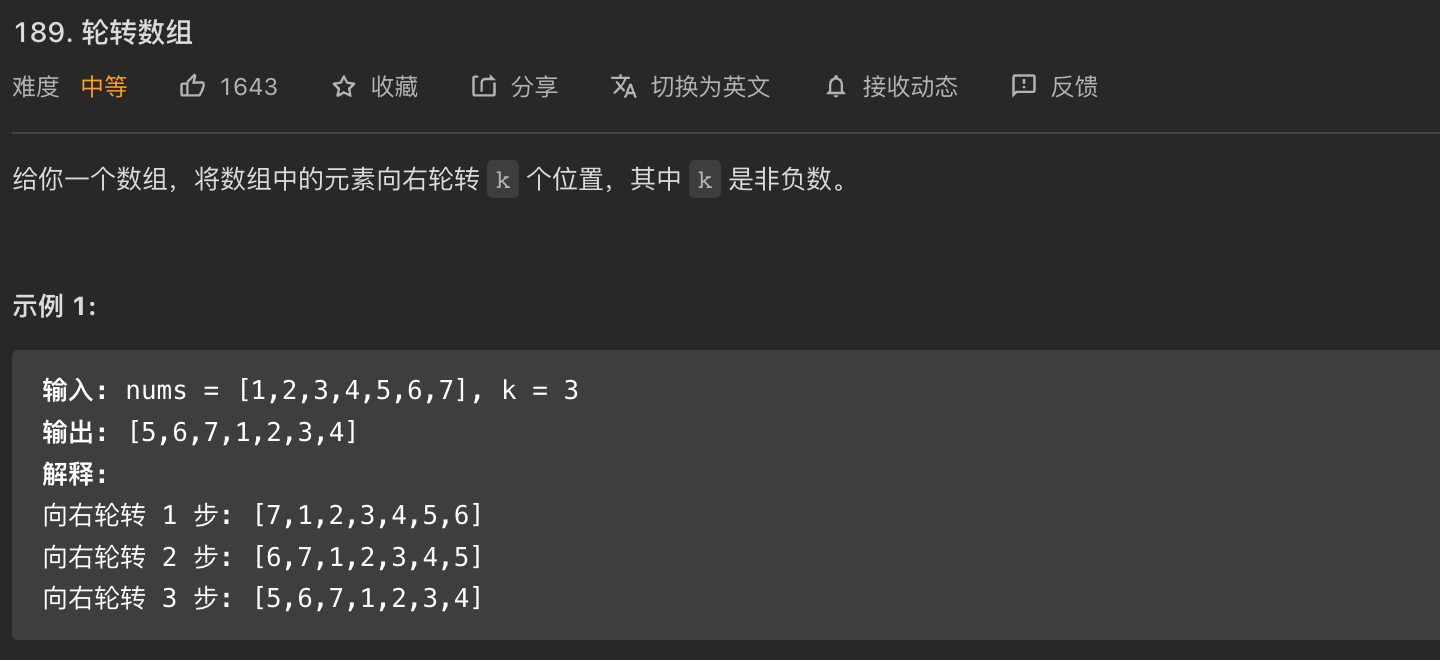
审题
- 需要思考的问题,想通过一次移位来解决,但需要确保移位后的 原来位置的元素的保存以及移位,要解决形成的递归关系难
1. 多次单次移位
超时
void rotate(int* nums, int numsSize, int k){
for(int i = 0; i < k; i++) {
rotateByOne(nums, numsSize);
}
}
void rotateByOne(int *nums, int numsSize) {
int temp = nums[numsSize - 1];
for(int i = numsSize - 1; i > 0; i--) {
nums[i] = nums[i-1];
}
nums[0] = temp;
}
2. 标志+双层前进
类似贪婪算法,维护一个当前的指标index,index前的元素都是已经右移k位的。如果对第index位,右移k位后,如果第 (index+k) % size位没有被右移,则将该位右移,依次迭代重复。时间复杂度在On
缺点:需要空间为On的数组来保存当前索引位上是否被右移的标志。
void rotate(int* nums, int numsSize, int k){
int index = 0;
int *bucket = (int *) (calloc(numsSize, sizeof(int)));
int x1, x2 = 0;
while(index < numsSize) {
int cur_index = index;
x1 = nums[cur_index];
while(bucket[cur_index] == 0) {
// exchange relavant nums
x2 = nums[(cur_index + k)%numsSize];
nums[(cur_index + k) % numsSize] = x1;
bucket[cur_index] = 1;
cur_index = (cur_index + k)%numsSize;
x1 = x2;
}
index++;
}
}
3. 双层移位+gcd
基于之前的递归类的右移,也就是一次性把一个索引位的元素 以及右移k位的元素 以及右移2k位的元素进行右移,也就是先处理一个循环周期内的元素.....这里主要分两类讨论,设元素个数为n,右移次数为k
- n 恰好能被k整除,即能在一趟跑遍 n/k个元素,需要跑k躺:
- n不能被k整除,分两种情况(其实合起来是一种情况):
- 一趟内跑遍n个元素,例如(n = 7, k=3)
- 一趟内跑不遍n个元素,只能跑完部分的元素,之后便会陷入重复(n = 8,k=6)
此时存在的数学关系: $$最终每个趟遍历元素数 = n / gcd(n, k) $$
此时就能在On的时间复杂度和O1的空间复杂度内解决问题(代码部分有待优化)
int gcd(int a, int b) {
int t = 1;
while(a % b) {
t = a%b;
a = b;
b = t;
}
return t;
}
void rotate(int* nums, int numsSize, int k){
if(k == 0) {
return nums;
}
int x1, x2, max = 0;
int out_foreach_count = k;
if(numsSize % k != 0) {
max = numsSize / gcd(numsSize, k);
out_foreach_count = numsSize / max;
}else{
max = numsSize / k ;
}
for(int i =0 ; i < out_foreach_count; i++) {
int count = 0;
int cur_index = i;
x1 = nums[cur_index];
while(count < max) {
// exchange relavant nums
x2 = nums[(cur_index + k)%numsSize];
nums[(cur_index + k) % numsSize] = x1;
cur_index = (cur_index + k)%numsSize;
x1 = x2;
count++;
}
}
}

4. 数组翻转(R)
LeetCode上提供的一种方法,也非常的巧妙。有时间可以再看一下。
198. 打家劫舍 ⭐⭐
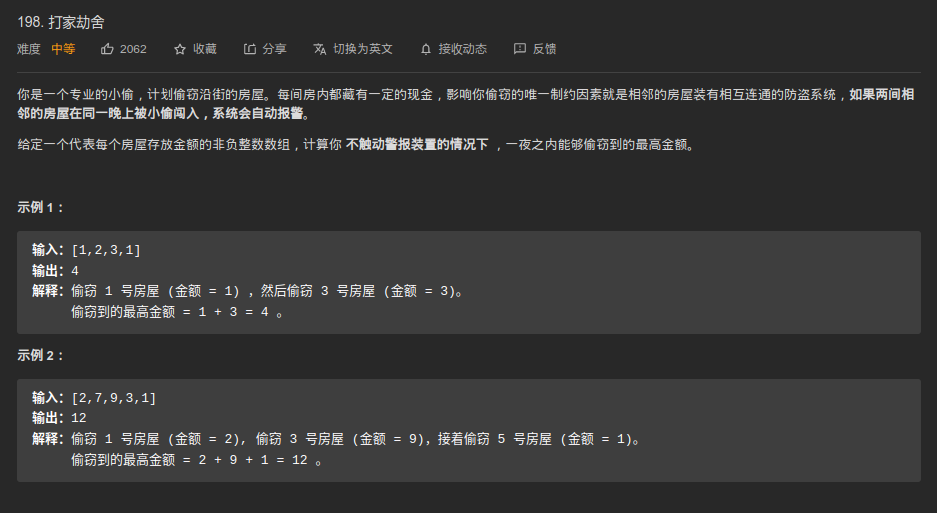
审题
- 不能在相邻的房间内偷窃,问题转换:判断一个数组在选定数无相邻情况下的和的最大值
- 特殊情况:可以一次跳多个数字,[6,1,2,9],这种情况就可以跳2格,因为1-2的值小于0
- 可能的算法:贪心?DP?
- 思路:
- 直接:
- DP:初始化数组,数组中的值还有是否拜访了当前值的标记,第n种的思路可以等于等1 ~ n-1种之和,取n-1时则其不能拜访当前的值
1. DP
贪心和DP的思想:我当前偷到第n户时我都保持了最大能偷的钱数,那么在偷第N+1家时,我需要注意:
- 是否能偷这家?也就是是否偷了上家
- 能偷则直接偷了因为肯定偷了比没偷好啊
- 不能偷,那要么不偷上家偷这家,要么偷上家不偷这家
- 偷上上家+偷这家的钱 > 偷上家不偷这家的钱,则偷这家钱的最大值就等于前者,并且还要说明偷了这家
- 偷上上家+偷这家的钱 < 偷上家不偷这家的钱,则偷这家钱的最大值等于后者
public int rob(int[] nums) {
if(nums.length == 1) {
return nums[0];
}
int i;
int[] isGo = new int[nums.length + 1];
int[] curMax = new int[nums.length + 1];
curMax[1] = nums[0];
isGo[1] = 1;
for(i = 2; i < nums.length + 1; i++) {
if(isGo[i - 1] == 1) {
if(curMax[i - 2] + nums[i - 1] < curMax[i - 1]) {
curMax[i] = curMax[i - 1];
}else{
curMax[i] = curMax[i - 2] + nums[i - 1];
isGo[i] = 1;
}
}else{
curMax[i] = curMax[i - 1] + nums[i - 1];
isGo[i] = 1;
}
}
return curMax[i - 1];
O(N)的时间复杂度 O(N)的空间复杂度
优化
DP从数组到常量个变量的经典优化:因为实际计算值只与curMax[i-1]、curMax[i-2]和isGo[i-1]有关,因此均可优化为常量级别的数组,以此降低空间复杂度到O(C) 。
public int rob(int[] nums) {
if(nums.length == 1) {
return nums[0];
}
int i;
int isGo = 0;
int[] curMax = new int[3];
curMax[1] = nums[0];
isGo = 1;
for(i = 1; i < nums.length; i++) {
if(isGo == 1) {
if(curMax[0] + nums[i] < curMax[1]) {
curMax[2] = curMax[1];
}else{
curMax[2] = curMax[0] + nums[i];
isGo = 1;
}
}else{
curMax[2] = curMax[1] + nums[i];
isGo = 1;
}
curMax[0] = curMax[1];
curMax[1] = curMax[2];
}
return curMax[2];
}
题解用Math.max优化了分支代码,取消了isGo的遍历,这个优化需要注意!使得代码非常简便
for (int i = 2; i < length; i++) {
int temp = second;
second = Math.max(first + nums[i], second);
first = temp;
}
再回首
public int rob(int[] nums) {
if(nums.length == 1) {
return nums[0];
}
// day_x: x-1 days ago
int day_3, day_2, day_1;
int i;
day_3 = nums[0];
day_2 = Math.max(nums[0], nums[1]);
day_1 = 0;
for(i = 2; i < nums.length; i++) {
day_1 = Math.max(day_3 + nums[i], day_2);
day_3 = day_2;
day_2 = day_1;
}
return day_2;
}
思路清晰了很多,先理清偷和不偷今天的盈利,然后考虑DP的数组形式,就能把大致思路想出来,再考虑DP的简化形式
总结
- 这道题做的很快,因为思路很清楚,为什么思路清楚?因为提到了钱,讨论钱的最大值再加上本身问题有迭代性质因素,所以想到了贪心和DP
- 然后先想清楚了大致思路才写的代码,把一些坑给避开了,这点很重要
206. 反转链表 ⭐
1. 迭代
public ListNode reverseList(ListNode head) {
ListNode cur = null;
ListNode pre = head;
ListNode temp=null;
try {
while (pre != null) {
temp = pre.next;
pre.next = cur;
cur = pre;
pre = temp;
}
}catch (NullPointerException e){
}
return cur;
}

2. 递归
public ListNode reverseList(ListNode head) {
ListNode cur=null;
try{
if(head.next==null||head==null){
return head;
}
cur=reverseList(head.next);
head.next.next=head;
head.next=null;
}catch(NullPointerException e){
}
return cur;
}

212. 单词搜索 II ⭐⭐⭐
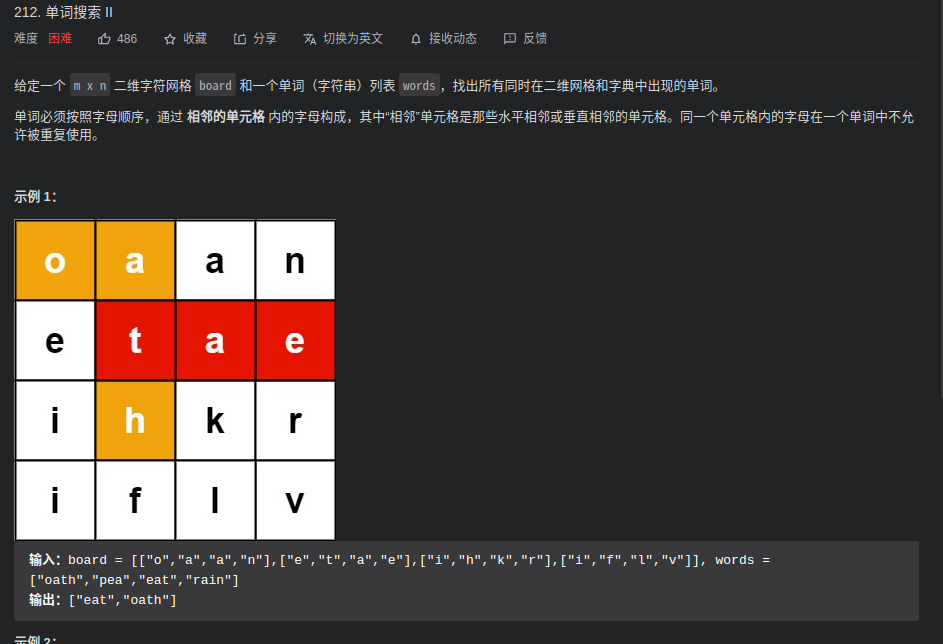
审题
- 单词必须按照字母顺序,通过 相邻的单元格 内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。
- 类似DFS?
- 这里每一个单词首字母寻找肯定要耗费时间,能不能用dp规划出每个字母的相邻位置的字母
- 注意相同字母可能在表中出现多次
1. 我的代码
这里没有做出来,因为后面涉及到了DFS,没有考虑到
public List<String> findWords(char[][] board, String[] words) {
int m = board.length;
int n = board[0].length;
int shouldExit = -1;
int index = 0;
List<String> result = new ArrayList<>();
char[][] dp = new char[m+2][n+2];
for(int i = 0 ;i < m+2; i++) {
for(int j = 0 ;j < n+2 ;j++) {
if(i==0||i==m+1||j==0||j==n+1){
dp[i][j] = ' ';
}else{
dp[i][j] = board[i-1][j-1];
}
}
}
for(int i = 1 ;i < m+1; i++) {
if(shouldExit == 1) {
break;
}
for(int j = 1 ;j < n+1 ;j++) {
if(dp[i][j] == words[index].charAt(0)) {
int wordsLength = 1;
int x = i;
int y = j;
int[][] his = new int[words[index].length][2];
his[0][0] = i;
his[0][1] = j;
while(true){
if(wordsLength == words[index].length()){
result.add(words[index]);
index++;
i = 0 ;
j = 0;
break;
}
int[] twin = isCharInAround(words[index].charAt(wordsLength),dp,x,y,his);
if(twin == null){
break;
}
his[wordsLength][0] = twin[0];
his[wordsLength][1] = twin[1];
x = twin[0];
y = twin[1];
wordsLength++;
}
}
if(i == m && j == n && index < words.length){
i = 0;
j = 0;
index++;
}
if(index == words.length) {
shouldExit = 1;
break;
}
}
}
return result;
}
public int[] isCharInAround(char target, char[][] board, int i, int j,int][] his) {
int[] res = new int[2];
res[0] = -1;
res[1] = -1;
if(board[i][j+1] == target) {
res[0] = i;
res[1] = j+1;
}else if(board[i][j-1] == target){
res[0] = i;
res[1] = j-1;
}else if(board[i+1][j] == target){
res[0] = i+1;
res[1] = j;
}else if(board[i-1][j] == target){
res[0] = i-1;
res[1] = j;
}
for(int i = 0; i< his.length; i++){
if(his[i][0] == res[0] && his[i][1] == res[1]) {
}
}
return res;
}
2. 前缀树+回溯 (转)
这里前缀树之前没了解过,看了下结构,不错
class Solution {
int[][] dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
public List<String> findWords(char[][] board, String[] words) {
Trie trie = new Trie();
for (String word : words) {
trie.insert(word);
}
// 细节,去重
Set<String> ans = new HashSet<String>();
for (int i = 0; i < board.length; ++i) {
for (int j = 0; j < board[0].length; ++j) {
dfs(board, trie, i, j, ans);
}
}
return new ArrayList<String>(ans);
}
public void dfs(char[][] board, Trie now, int i1, int j1, Set<String> ans) {
if (!now.children.containsKey(board[i1][j1])) {
return;
}
char ch = board[i1][j1];
now = now.children.get(ch);
if (!"".equals(now.word)) {
ans.add(now.word);
}
// 避免找到重复的位置(也是我思路中卡壳的地方)
board[i1][j1] = '#';
for (int[] dir : dirs) {
int i2 = i1 + dir[0], j2 = j1 + dir[1];
if (i2 >= 0 && i2 < board.length && j2 >= 0 && j2 < board[0].length) {
dfs(board, now, i2, j2, ans);
}
}
// 还原
board[i1][j1] = ch;
}
}
class Trie {
String word;
Map<Character, Trie> children;
boolean isWord;
public Trie() {
this.word = "";
this.children = new HashMap<Character, Trie>();
}
public void insert(String word) {
Trie cur = this;
for (int i = 0; i < word.length(); ++i) {
char c = word.charAt(i);
if (!cur.children.containsKey(c)) {
cur.children.put(c, new Trie());
}
cur = cur.children.get(c);
}
cur.word = word;
}
}
复杂度分析

有时间得看一下前缀树,常用于字符串的查找,以后遇到这种问题可以纳入考虑
3. 删除被匹配的单词
213. 打家劫舍 II ⭐⭐
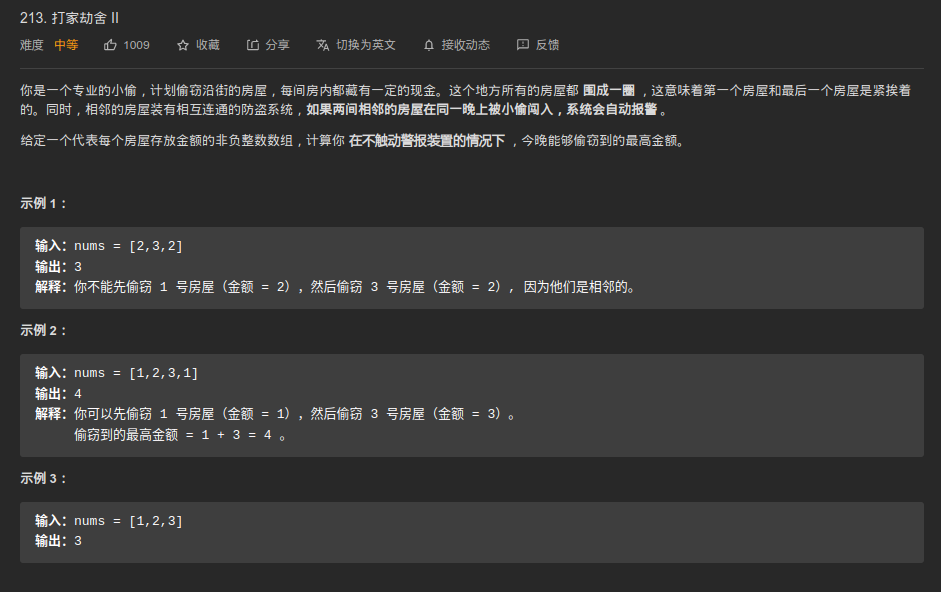
审题
- 房屋围成一圈,不能偷相邻的
1. DP (转)
寄,想复杂了。。。。。
其实只有三种情况:
- 房间数=1,则就直接偷
- 房间数=2,选最多钱的偷
- 房间数>2,看偷不偷第一家
- 偷第一家,则不能偷最后一家
- 不偷一家,则能够偷(但不一定会偷)最后一家
class Solution {
public int rob(int[] nums) {
int length = nums.length;
if (length == 1) {
return nums[0];
} else if (length == 2) {
return Math.max(nums[0], nums[1]);
}
return Math.max(robRange(nums, 0, length - 2), robRange(nums, 1, length - 1));
}
public int robRange(int[] nums, int start, int end) {
int first = nums[start], second = Math.max(nums[start], nums[start + 1]);
for (int i = start + 2; i <= end; i++) {
int temp = second;
second = Math.max(first + nums[i], second);
first = temp;
}
return second;
}
}
反思
- 这个题自己想复杂了,想成循环链表又想到如何动态规划
- 没有关注相比 I 题变换的本质:仅仅是首尾的变换,不影响中间元素。
219. 存在重复元素II ⭐
⏲️ 2022 / 1 / 19 11:30 AM
审题
- 可能做法: 遍历肯定行;双指针?滑动窗口?栈?
- 注意:不必完全找出来所有的可能啊!
- 有点抽屉原理的感觉
1. 遍历
对数组进行遍历,对每一个 i 向前看k个数,最终得到时间复杂度为$$O(N * K)$$
似乎还行?
public boolean containsNearbyDuplicate(int[] nums, int k) {
for(int i = 0; i < nums.length; i++) {
for(int j = i+1; j < nums.length && j <= i + k; j++) {
if(nums[i] == nums[j]) {
return true;
}
}
}
return false;
}
寄,当K接近N的时候,就变成$$O(N^2)$$的时间复杂度了,慢是正常的....考虑下一种
2. 哈希
public boolean containsNearbyDuplicate(int[] nums, int k) {
Map<Integer, Integer> hashmap = new HashMap<>();
for(int i = 0; i < nums.length; i++) {
int temp = hashmap.getOrDefault(nums[i], -1);
if(temp == -1) {
hashmap.put(nums[i], i);
}else {
if(i - temp <= k)
return true;
hashmap.put(nums[i], i);
}
}
return false;
}
On的时间复杂度,On以上的空间复杂度(哈希表扩容),时间还是比较慢
优化后
set保证单一
remove保证没有过期元素
public boolean containsNearbyDuplicate(int[] nums, int k) {
HashSet<Integer> set = new HashSet<>();
for(int i = 0; i < nums.length; i++) {
if(set.contains(nums[i])) {
return true;
}
set.add(nums[i]);
if(set.size() > k) {
set.remove(nums[i - k]);
}
}
return false;
}
3. 桶
int max, min;
max = min = nums[0];
for(int i = 0; i < nums.length; i++) {
if(nums[i] > max)
max = nums[i];
if(nums[i] < min)
min = nums[i];
}
int[] bucket = new int[max - min + 1];
for(int i = 0; i < bucket.length; i++) {
bucket[i] = -1;
}
for(int i = 0; i < nums.length; i++) {
int temp = bucket[nums[i] - min];
if(temp == -1) {
bucket[nums[i] - min] = i;
}else {
if(i - bucket[nums[i] - min] <= k)
return true;
bucket[nums[i] - min] = i;
}
}
return false;
失败,超出内存限制
4. 排序
O(N * (logN))的快排,然后遍历比较就行
还需要一个数组来维护索引的顺序 On的空间复杂度
5. 滑动窗口 + Hash(转)
遍历过程中用哈希表存储元素并同时判断窗口大小是否超过了K。用哈希Set这里也就不用自己判断了
public boolean containsNearbyDuplicate(int[] nums, int k) {
Set<Integer> cache = new HashSet<>();
for (int i = 0; i < nums.length; i++) {
if (i - k > 0) {
cache.remove(nums[i - k - 1]);
}
if (!cache.add(nums[i])) {
return true;
}
}
return false;
}
牛逼.....
总结
这里最开始做的时候思路大体是对的,要数字决定的索引之间的差值关系,就考虑用桶或者哈希,但自己用了哈希后感觉用桶排序会更快,但后面一直纠结实现桶排序但未考虑最大值而超出了内存限制。感觉自己还是一直纠结把索引保存下来,但其实这里不用保存索引关系,考虑了滑动窗口的问题只需要留一段窗口内的值就行了呀......
- 看到值决定的索引间关系问题考虑用哈希
- 重复元素判别问题考虑Set,可能比Hash快
- 数组一定范围内的问题考虑滑动窗口,滑动窗口实现方式可以是多种多样的,不一定是数组哦!
223. 矩形面积 ⭐⭐
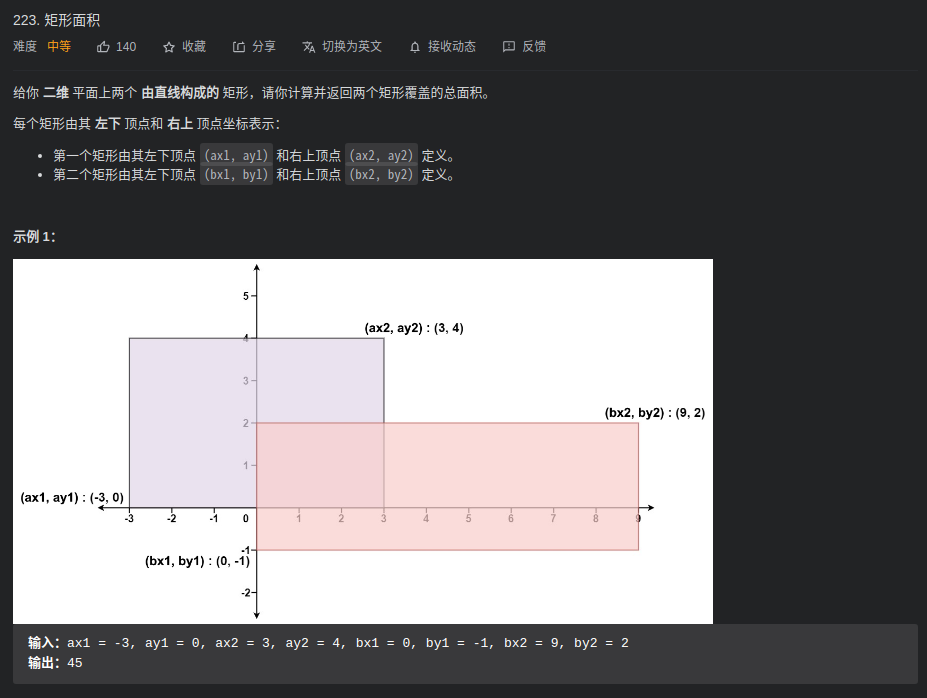
审题
- 两种情况:
- 未覆盖
- 覆盖(可能完全包含)
- 如何判断是否覆盖?
- 关键: 如何计算覆盖区域的面积?
- 难道是模拟? 分类太多,直接放弃
260. 只出现一次的数字III ⭐⭐
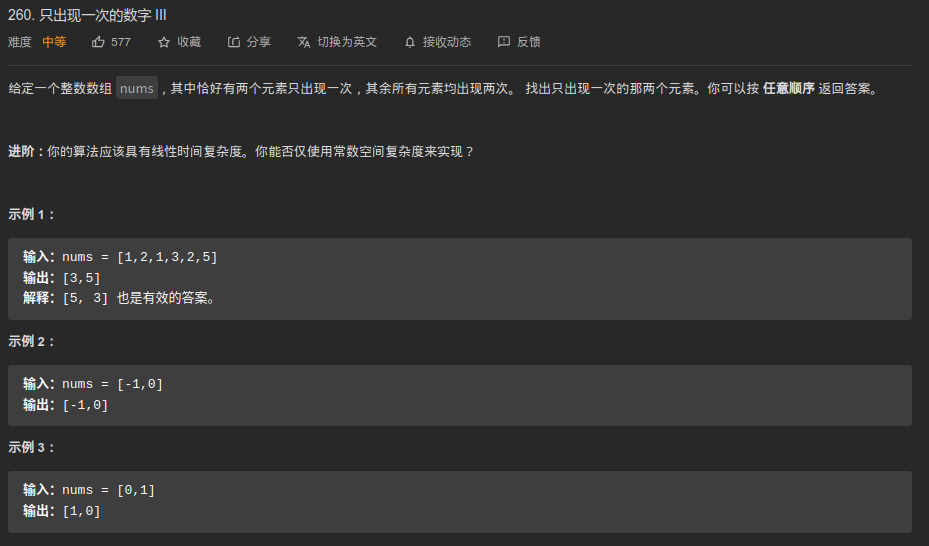
审题
- 恰好两个元素只出现一次,其他元素均出现两次;数组 ---> 一次遍历即为较优秀的算法
- 考虑线性时间复杂度的算法和常数空间复杂度
- 可能的做法:哈希
- 想法:
- 简单:暴力循环。需要O(n^2)的时间复杂度
- 进阶:哈希两次外循环,需要O(n)时间复杂度和O(n)空间复杂度
- 高级:On的空间复杂度,想不出来.....
1. 哈希 两次遍历
第一次遍历填值,第二次遍历判断
public int[] singleNumber(int[] nums) {
HashMap<Integer,Integer> map = new HashMap<>();
int[] res = new int[2];
for(int i = 0; i < nums.length; i++) {
map.put(nums[i], map.getOrDefault(nums[i],0) + 1);
}
int index = 0;
for(int i = 0; i < nums.length; i++) {
if(map.get(nums[i]) == 1) {
res[index] = nums[i];
index++;
}
}
return res;
}
On的时间复杂度,但受到Map扩容方面的问题
2. 位运算(转)
直接忘得一干二净,之前还专门有做过一模一样的题,忘了。比较有技巧性。一个异或的公式说明一切问题:
class Solution {
public int numSquares(int n) {
int[] dp = new int[n + 1]; // 默认初始化值都为0
for (int i = 1; i <= n; i++) {
dp[i] = i; // 最坏的情况就是每次+1
for (int j = 1; i - j * j >= 0; j++) {
dp[i] = Math.min(dp[i], dp[i - j * j] + 1); // 动态转移方程
}
}
return dp[n];
}
}
On的空间复杂度 Onlogn的时间复杂度
2. BFS + 剪枝 (转)
BFS确保了当到这一层时,如果为余数为0,则一定是最小的数目。
注意这里visited确保的是不重复,第二层有一个3,第三层又有一个3,那肯定还是第二层的3的数目<走第三层的3的数目,所以没必要要第三层的。
public int numSquares(int n) {
Queue<Integer> queue = new LinkedList<>();
Set<Integer> visited = new HashSet<>();
int level = 1;
queue.offer(n);
visited.add(n);
while(!queue.isEmpty()) {
int size = queue.size();
// 经典做法,用来控制每层的循环的
for(int i = 0; i < size; i++) {
int head = queue.poll();
int sq = (int)Math.sqrt(head);
for(int j = 1; j <= sq; j++) {
int tmp = head - j * j;
// 找到了第一个全由 完全平方数 组成的组合,减到0了已经
if(tmp == 0) {
return level;
}
// 比如同一层,已经有了1个1,那就不需要再放进去了
// 因为都在同一层,往后的层数结果肯定是一样的啊,就是剪枝!!!
if(!visited.contains(tmp)) {
visited.add(tmp);
queue.offer(tmp);
}
}
}
level++;
}
return level;
}
空间复杂度大于On
时间复杂度On?
3. 数学公式 (转)
四平方和定理:任意一个正整数都可以被表示为至多四个正整数的平方和。当前仅当$$n \neq 4^k \times (8m+7) $$,n可以被表示为至多三个正整数的平方和,而如果相等时,则n仅可以表示为四个正整数的平方和
由以上定理,则N !=...时,有三种情况:
- 1种,则必为n的完全平方数
- 2种,n = a^2 + b^2 ,只需要枚举所有的a,判断n - a^2是否为完全平方数即可
- 3种,排除法
空间复杂度 O1
时间复杂度 $$O(\sqrt n)$$
总结
做这一题的时候思路大概上还是对的,想到了动态规划,之后想到了自定义链表进而想到了DFS,但这道题是BFS解的......
- 从树的角度:对多叉树的层数解法考虑BFS
- 从数组的角度:后一个值依赖于前几个值,考虑dp
292. Nim游戏 ⭐⭐
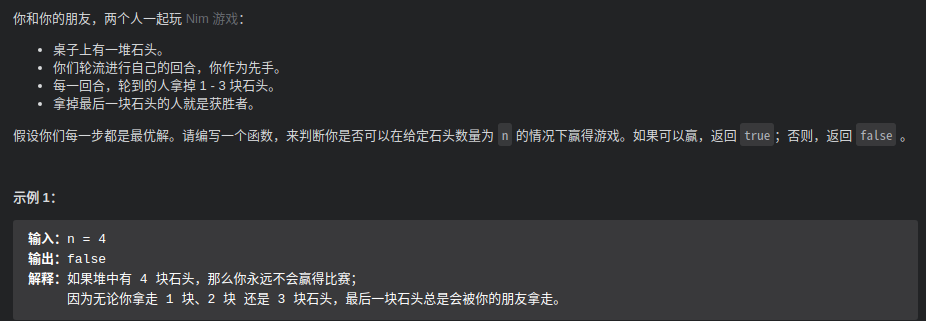
审题
- “你作为先手”
- 两个人,双方都尽力向拿走全部石头
- “是否” ,“如果”
- 递归?树?
Failed:没做出来,一直抓着递归来做,在“如何聪明的判断剩下的石头是否能完全使对方输掉”这个问题上纠结。。
1. 数学推理(转)
/*
让我们考虑一些小例子。显而易见的是,如果石头堆中只有一块、两块、或是三块石头,那么在你的回合,你就可以把全部石子拿走,从而在游戏中取胜;如果堆中恰好有四块石头,你就会失败。因为在这种情况下不管你取走多少石头,总会为你的对手留下几块,他可以将剩余的石头全部取完,从而他可以在游戏中打败你。因此,要想获胜,在你的回合中,必须避免石头堆中的石子数为 44 的情况。
我们继续推理,假设当前堆里只剩下五块、六块、或是七块石头,你可以控制自己拿取的石头数,总是恰好给你的对手留下四块石头,使他输掉这场比赛。但是如果石头堆里有八块石头,你就不可避免地会输掉, ********因为不管你从一堆石头中挑出一块、两块还是三块,你的对手都可以选择三块、两块或一块,以确保在再一次轮到你的时候,你会面对四块石头*********。显然我们继续推理,可以看到它会以相同的模式不断重复 n = 4, 8, 12, 16, \ldotsn=4,8,12,16,…,基本可以看出如果堆里的石头数目为 44 的倍数时,你一定会输掉游戏。
如果总的石头数目为 44 的倍数时,因为无论你取多少石头,对方总有对应的取法,让剩余的石头的数目继续为 44 的倍数。对于你或者你的对手取石头时,显然最优的选择是当前己方取完石头后,让剩余的石头的数目为 44 的倍数。假设当前的石头数目为 xx,如果 xx 为 44 的倍数时,则此时你必然会输掉游戏;如果 xx 不为 44 的倍数时,则此时你只需要取走 x \bmod 4xmod4 个石头时,则剩余的石头数目必然为 44 的倍数,从而对手会输掉游戏。
*/
public boolean canWinNim(int n) {
return n % 4 != 0;
}
这里还是通过特殊情况4的判断,咬定了4作为唯一的特殊情况,延伸推理出4的倍数。比较巧妙的是
- 先手
- 由于先手,无论你拿几个,只要我保证在4的倍数,就无法取得胜利
300. 最长递增子序列 ⭐⭐
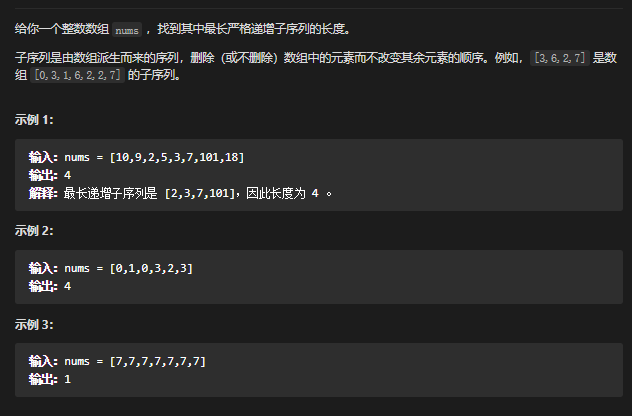
思考
可以不连续, 动态规划 dp 通项式
1. 自己写的dp
int[] dp = new int[nums.length];
int max = Integer.MIN_VALUE;
dp[0] = 1;
for(int i = 0; i<nums.length; i++){
int k = 0;
int inmax = Integer.MIN_VALUE;
for(int j = 0; j<i; j++){
if(nums[j]<nums[i] && nums[j]>inmax ){
inmax = nums[j];
k = j;
}
if(inmax != Integer.MIN_VALUE&& dp[k] < dp[j]&& nums[j] < nums[i]){
k = j;
inmax = nums[j];
}
}
if(inmax == Integer.MIN_VALUE) dp[i] = 1;
else if(nums[k] == nums[i]) dp[i] = dp[k];
else dp[i] = dp[k] + 1;
if(max<=dp[i]){
max = dp[i];
}
}
return max;
条件判断太多了 辣鸡
时间复杂度 O(n2)
2. 真正的dp
class Solution {
public int lengthOfLIS(int[] nums) {
if (nums.length == 0) {
return 0;
}
int[] dp = new int[nums.length];
dp[0] = 1;
int maxans = 1;
for (int i = 1; i < nums.length; i++) {
dp[i] = 1;
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
maxans = Math.max(maxans, dp[i]);
}
return maxans;
}
}
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/longest-increasing-subsequence/solution/zui-chang-shang-sheng-zi-xu-lie-by-leetcode-soluti/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。

贪心+二分
没看懂 -------

class Solution {
public int lengthOfLIS(int[] nums) {
int len = 1, n = nums.length;
if (n == 0) {
return 0;
}
int[] d = new int[n + 1];
d[len] = nums[0];
for (int i = 1; i < n; ++i) {
if (nums[i] > d[len]) {
d[++len] = nums[i];
} else {
int l = 1, r = len, pos = 0; // 如果找不到说明所有的数都比 nums[i] 大,此时要更新 d[1],所以这里将 pos 设为 0
while (l <= r) {
int mid = (l + r) >> 1;
if (d[mid] < nums[i]) {
pos = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
d[pos + 1] = nums[i];
}
}
return len;
}
}
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/longest-increasing-subsequence/solution/zui-chang-shang-sheng-zi-xu-lie-by-leetcode-soluti/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
322. 零钱兑换 ⭐⭐
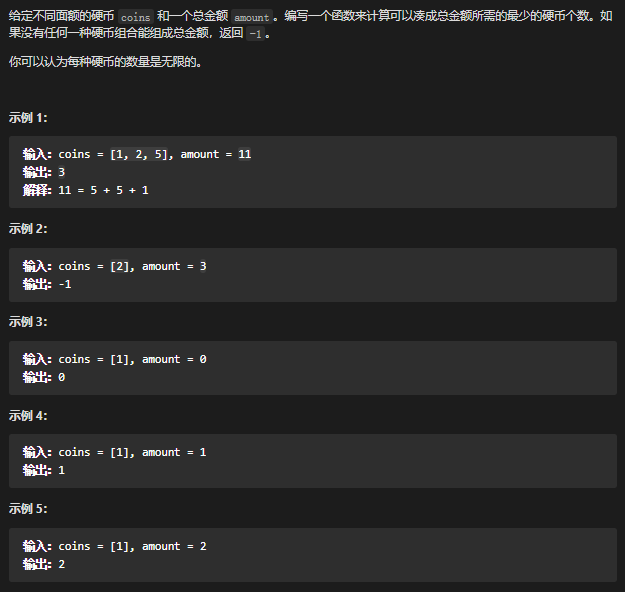
思考
没有想dp ....很拉 有想到DFS 不过没有实现
1. 记忆DFS
2. DP
326. 3的幂 ⭐
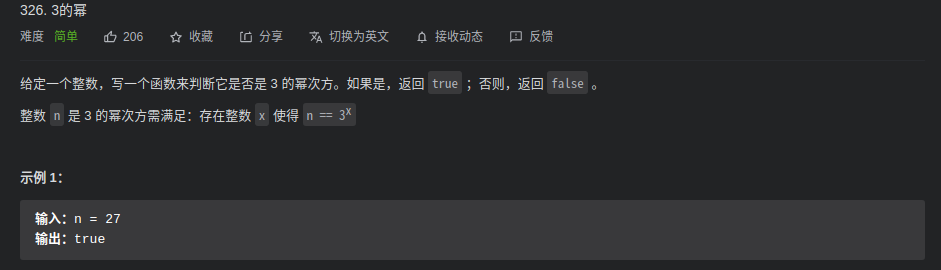
审题
- 递归
- 迭代
- 位运算?
1. 递归
public boolean isPowerOfThree(int n) {
if(n == 3 || n == 1) {
return true;
}
if(n % 3 != 0 || n == 0) {
return false;
}
return isPowerOfThree(n / 3);
}

2. 迭代
public boolean isPowerOfThree(int n) {
while(true) {
if(n == 3 || n == 1){
break;
}
if(n % 3 != 0 || n == 0) {
return false;
}
n = n / 3;
}
return true;
}
337. 打家劫舍III⭐⭐
思考
- 打劫这一家 或者
1. DFS(超时)
- 对当前元素,先看其父元素是否被偷窃,如果被偷,说明不能偷这个元素,并且**可以偷也可以不偷(不属于这次管)**该元素的子元素,从偷和不偷子元素的两种方案中原则最大的一种;
- 如果父元素没有被偷,则可以偷这个元素,也可以不偷这个元素
- 最终取偷该元素和不偷该元素所带来的最大值
class Solution {
public int rob(TreeNode root) {
return robByFlag(root, true);
}
public int robByFlag(TreeNode root, boolean flag) {
if(root == null)
return 0;
// can rob this house
int count_1, count_2;
if(flag) {
count_1 =robByFlag(root.left, false) + robByFlag(root.right, false) + root.val;
}else{
count_1 = 0;
}
count_2 = robByFlag(root.left, true) + robByFlag(root.right, true);
return Math.max(count_1, count_2);
}
}
2. DP+DFS(转)
f(o)表示选中当前节点 g(o)表示不选中当前节点
- 当父元素o被选中时,o的左右孩子不能被选中,o被选中的情况下以o为根节点的树的最大权值之和为其左孩子的最大权值 + 右孩子的最大权值 $f(o) = g(l) + g(r) $
- o不被选中时,o的左右孩子能被选中,也可以不被选中,此时$ g(o) = max{f(l), g(l)} + max{f(r), g(r)} $;
所以可以用哈希表存取每个节点的f值和g值,用DFS遍历得到g和f中每个节点对应的值
class Solution {
Map<TreeNode, Integer> f = new HashMap<TreeNode, Integer>();
Map<TreeNode, Integer> g = new HashMap<TreeNode, Integer>();
public int rob(TreeNode root) {
dfs(root);
return Math.max(f.getOrDefault(root, 0), g.getOrDefault(root, 0));
}
public void dfs(TreeNode node) {
if(node == null) {
return;
}
dfs(node.left);
dfs(node.right);
f.put(node, node.val + g.getOrDefault(node.left, 0) + g.getOrDefault(node.right, 0));
g.put(node, Math.max(f.getOrDefault(node.left, 0), g.getOrDefault(node.left, 0)) + Math.max(f.getOrDefault(node.right, 0), g.getOrDefault(node.right, 0)));
}
}
344. 反转字符串 ⭐
我的代码:
一次遍历
static void reverse(char[] s){
//一次遍历? 空间复杂度O(n)=1 ,时间复杂度O(n)=n;
char temp;
for(int i=0;i<s.length/2;i++){
temp=s[i];
s[i]=s[s.length-i-1];
s[s.length-i-1]=temp;
}
}
递归法
static char[] reverse_1(char[]s, int left, int right){
//递归法
if(left<right) {
char temp;
temp = s[left];
s[left] = s[right];
s[right] = temp;
return reverse_1(s, left + 1, right - 1);
}
return s;
}
计算结果:
一次遍历

递归

分析思考:
1. 双指针 方法, 指向头尾指针,两标兵向中部靠齐,if循环和while判断都可以
2. 采用递归,内存占用会高一点 ,执行用时也非常慢
357. 统计各位数字都不同的的数字个数 ⭐⭐
审题
只有位数有两个位数相同则就不满足,给定的n代表10的n次方
思路:
直接:
- 按十进制拆分比较,递归\迭代,但各位数字
进阶:
数学公式:100以内有9个(因为十位和个位)
1000以内有(十位个位+个位百位十位百位+个位十位百位)但要区分冗余- 两位重复:也就是每两位重复的总数为9 * 9 * 2 + 9 * 9 2
- 三位重复:9
对4位数来说:
- 两位重复:
3 * (9 * 9 * 8 ) + 3 * (9 * 8 * 9) - 三位重复:2 * 9 * 9+ 2 * (9 * 9 )
- 四位重复:9
1. 按十进制遍历(OverTime)
按照十进制位数去取,然后通过bucket来哈希判断是否重复,超时,意料之中
public int countNumbersWithUniqueDigits(int n) {
if(n == 0) {
return 1;
}
if(n == 1) {
return 10;
}
int res = 11;
int max = (int) Math.pow(10,n);
for(int i = 11; i < max; i++) {
int temp = i;
int flag = 1;
int[] buc = new int[10];
while(temp != 0) {
if(buc[temp % 10] != 0) {
flag = 0;
break;
}
buc[temp % 10]++;
temp /= 10;
}
res += flag;
}
return res;
}
2. 排列组合(转)
对n > 1的情况,n由n-1的值(0 ~ 10 ^ (n-2)) 再 加上 (10 ^(n-1) ~ 10 ^(n - 1))决定,也就是个位为1-9,不为0,则剩下的位数则只能有9 - 8 - 7 ....种取法,(注意 n > 8后必然会有重复取值,所以最大值在n = 8时取得)。 这里的做法其实也可以有dp的思想
class Solution {
public int countNumbersWithUniqueDigits(int n) {
if (n == 0) {
return 1;
}
if (n == 1) {
return 10;
}
int res = 10, cur = 9;
for (int i = 0; i < n - 1; i++) {
cur *= 9 - i;
res += cur;
}
return res;
}
}
// 作者:LeetCode-Solution
// 链接:https://leetcode-cn.com/problems/count-numbers-with-unique-digits/solution/tong-ji-ge-wei-shu-zi-du-bu-tong-de-shu-iqbfn/
耗时就不看了 100%。这道题自己做的很遭,最开始 是想算出每一层的不满足条件的数,就分了很多种情况,想累加到一起,但一直有个差一些,不知道是哪里算错了。题解用正向求解的方法结合排列组合做起来就很容易,自己那种方法想了很久还想不对
反思!之后发现错误来源,对四位数,只有2位重复的,我考虑了aabc这种类型,却没有考虑aabb这种类型,也是2位重复的,导致我算的结果一直比正确结果少了243,正面去证明确实不是很好说明
反思
- 别看的太细致,有时候宏观考虑
371. 两整数之和 (R) ⭐⭐
审题
- 位运算
1. 二进制计算器
public int getSum(int a, int b) {
int[] aArr = getBinaryArr(a);
int[] bArr = getBinaryArr(b);
int[] maxArr;
int[] minArr;
if((aArr.length > bArr.length)) {
maxArr = aArr;
minArr = bArr;
} else{
maxArr = bArr;
minArr = aArr;
}
int[] res = new int[maxArr.length + 1];
boolean needUp = false;
for(int i = 0; i < minArr.length; i++) {
if(!needUp) {
if((maxArr[i] & minArr[i]) == 1) {
needUp = true;
res[i] = 0;
}else{
res[i] = maxArr[i] | minArr[i];
}
}else{
if((maxArr[i] & minArr[i]) == 1) {
needUp = true;
res[i] = 1;
}else if((maxArr[i] | minArr[i]) == 1){
res[i] = 0;
needUp = true;
}else{
res[i] = 1;
needUp = false;
}
}
}
for(int i = minArr.length ; i < maxArr.length; i++) {
if(needUp) {
if(maxArr[i] == 0) {
res[i] = 1;
needUp = false;
}else{
res[i] = 0;
}
}else{
res[i] = maxArr[i];
}
}
if(needUp) {
res[res.length - 1] = 1;
}
return getDenNum(res);
}
public int[] getBinaryArr(int num) {
int origin = num;
int i = 0;
int len = (int) (Math.log((double)num) / Math.log(2)) + 1;
int[] arr = new int[32];
int index = 0;
origin = Math.abs(num);
while(origin != 0) {
i = origin % 2;
origin /= 2;
arr[index] = i;
index ++;
}
if(num < 0) {
boolean needUp = false;
arr[31] = 1;
for(int j = 0; j < arr.length - 1; j++) {
arr[j] = 1 - arr[j];
}
if(arr[0] == 0){
arr[0] = 1;
}else{
arr[0] = 0;
int d = 1;
needUp = true;
while(needUp) {
if(arr[d] == 1){
arr[d] = 0;
}else{
arr[d] = 1;
needUp = false;
}
d++;
}
}
}
return arr;
}
public int getDenNum(int[] arr) {
int res = 0;
int mi = 1;
for(int i = 0; i < arr.length; i++) {
if(arr[i] == 1){
res+=mi;
}
mi *= 2;
}
return res;
}
这里主要通过将a,b两数字拆分成二进制进行相加,在二进制层面进行数的运算
做题所用的时间太久了,这里主要的问题包括
- 未考虑清楚正、负的加减情况,生成二进制数时应该要对其进行正负的判断并且转换
- 未使用副本(num =/ 2)。直接使用原数进行运算,后面就造成了错误答案
2. 位运算(转)
还是不太懂这里的算法。。。
public int getSum(int a, int b) {
while (b != 0) {
int carry = (a & b) << 1;
a = a ^ b;
b = carry;
}
return a;
}
于是,我们可以将整数 a 和 b 的和,拆分为 a 和 b 的无进位加法结果与进位结果的和。
同时,异或运算^ 经常用于无进位加法
373. 查找和最小的K对数字 ⭐⭐
审题
- 数组是升序排列
- 双指针?比较多个数?如何记住已经选了的数?(和相等的时候无法判断)
- 对索引为 i 的数组1和索引为 j 的数组2,有如下情况:
- j + 1 ,比较 i = 0
- i + 1 ,比较 j = 0
- 以上情况都要考虑是否重复,且如果j或者i = nums.length的时候,要考虑重置
1. 优先队列(转)
public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
PriorityQueue<int[]> pq = new PriorityQueue<int[]>(k,(o1,o2)->{
return nums1[o1[0]] +nums2[o1[1]] - nums1[o2[0]] - nums2[o2[1]];
});
// 先指定Comparator规则
List<List<Integer>> res = new ArrayList<List<Integer>>();
for(int i = 0; i < Math.min(nums1.length, k); i++) {
pq.offer(new int[]{i,0});
// 避免矛盾或冗余
}
// 注意这里放在temp中的是索引而不是值!
while(k-- > 0 && !pq.isEmpty()) {
int[] idxPair = pq.poll();
List<Integer> temp = new ArrayList<Integer>();
temp.add(nums1[idxPair[0]]);
temp.add(nums2[idxPair[1]]);
res.add(temp);
// 关键。实现了延续判断后面的值
if(idxPair[1] + 1 < nums2.length) {
pq.offer(new int[]{idxPair[0], idxPair[1] + 1});
}
}
return res;
}
这题用优先队列的方法有道理。带Comparator的优先队列能保证在指定的一段序列中肯定是最小的那个先出去,自然实现了排序;并且先加入一段序列,消除了去重问题;我考虑的不同情况的判断也在这里得到消除;
时间复杂度 k · Logk
延伸:学习一下PriorityQueue的siftUp
2. 二分法(转)
找到最佳近似值,得到所有小于的数对 ,找到相等的值的数对
380. O(1)时间插入、删除和获取随机元素 ⭐⭐
审题
- 插入-删除元素存在-不存在时,返回false
- 随机返回,可以用之前学的抹除?
- 思路:
- 插入和删除都要判断是否存在,所以O1时间内,应该用哈希表
- 主要在于随机返回是基于哈希表的,如何在O1时间内返回?
1. 哈希表+Random
Set存有效值,Map去根据顺序保存当前插入顺序为Key的值,随机查找不能在O1的时间内返回,且不是随机概率的,所以答案是无效的
class RandomizedSet {
Set<Integer> set;
Map<Integer,Integer> map;
int size;
Random rand;
public RandomizedSet() {
set = new HashSet<>();
map = new HashMap<>();
rand = new Random();
size = 0;
}
public boolean insert(int val) {
if(!set.contains(val)) {
set.add(val);
map.put(size++,val);
return true;
}
return false;
}
public boolean remove(int val) {
if(set.contains(val)) {
set.remove(val);
return true;
}
return false;
}
public int getRandom() {
int randNum = rand.nextInt(size);
while(!set.contains(map.get(randNum))) {
randNum = rand.nextInt(size);
}
return map.get(randNum);
}
}
382. 链表随机节点 ⭐⭐

已知数据有限对大数据的随机化问题的解决
审题
每个节点被选中的概率一样
Solution 是一个单独类,可以内含自己的数据结构
如何实现随机化吗?
做法:Random函数解决肯定太简单了。
1. API使用
ArrayList 和 Random联用
class Solution {
List<Integer> arr;
Random rand;
public Solution(ListNode head) {
ListNode temp = head;
rand = new Random();
arr = new ArrayList<Integer>();
while(temp != null) {
arr.add(temp.val);
temp = temp.next;
}
}
public int getRandom() {
int i = rand.nextInt(arr.size());
// int i =(int) Math.floor((Math.random() * arr.size()));
return arr.get(i);
}
}
虽然用了API,但结果看起来还不错.......缺点:在初始化时会遍历所有的节点,有LogN的时间复杂度,不切实际
去掉Random类改用Math的random方法使内存消耗略有提升
总的来说:
时间复杂度:初始化为On 选择时O1
空间复杂度:On
2. 蓄水池(转)
这里的问题主要是在仅能够读取1个数据的时候,如何实现大数据中的随机化问题。关键看这里如何保证了循环时取数据的平等概率

class Solution {
ListNode inner;
Random random;
public Solution(ListNode head) {
inner = head;
random = new Random();
}
public int getRandom() {
int i = 0;
ListNode temp = inner;
int res = temp.val;
while(temp != null) {
i++;
if(random.nextInt(i) == 0) {
res = temp.val;
}
temp = temp.next;
}
return res;
}
}
417. 太平洋大西洋水流问题 ⭐⭐

审题
- 理清思路:
- 如何判断是到大西洋还是太平洋?
- 左上方 (i == 0 || j == 0) && value > 0
- 右下方 (i == m - 1 || j == n - 1) && value > 0
- 核心问题,找到一条路径能够让当前元素的值分配1个点在其他较小元素且能到达边界
- 如何判断是到大西洋还是太平洋?
1. DFS
class Solution {
public List<List<Integer>> pacificAtlantic(int[][] heights) {
List<List<Integer>> res = new ArrayList<>();
List<Integer> temp;
for(int i = 0; i < heights.length; i++) {
for(int j = 0; j < heights[0].length; j++) {
if(canGetPacific(heights, i, j, true) && canGetPacific(heights, i, j, false)) {
temp = new ArrayList<>();
temp.add(i);
temp.add(j);
res.add(temp);
}
}
}
return res;
}
public boolean canGetPacific(int[][] heights, int i, int j, boolean mode) {
if(heights[i][j] < 0) {
return false;
}
if(mode) {
if(i == 0 || j == 0) {
return true;
}
}else{
if(i == heights.length - 1 || j == heights[0].length - 1) {
return true;
}
}
int temp = heights[i][j];
boolean canGet = false;
if(i-1 >= 0 && heights[i-1][j] != -1 && heights[i-1][j] <= heights[i][j]) {
heights[i][j] = -1;
canGet = canGetPacific(heights,i - 1 , j, mode);
heights[i][j] = temp;
}
if(!canGet && i + 1 < heights.length && heights[i+1][j] != -1 && heights[i+1][j] <= heights[i][j]) {
heights[i][j] = -1;
canGet = canGetPacific(heights,i + 1 , j, mode);
heights[i][j] = temp;
}
if(!canGet && j - 1 >= 0 && heights[i][j-1] != -1 && heights[i][j-1] <= heights[i][j]) {
heights[i][j] = -1;
canGet = canGetPacific(heights,i , j - 1, mode);
heights[i][j] = temp;
}
if(!canGet && j + 1 < heights[0].length && heights[i][j + 1] != -1 && heights[i][j+1] <= heights[i][j]) {
heights[i][j] = -1;
canGet = canGetPacific(heights,i , j + 1, mode);
heights[i][j] = temp;
}
return canGet;
}
}
Map优化
效果不明显
if(map.get(i*(heights[0].length) + j) != null && map.get(i*(heights[0].length) + j) == 1) {
return true;
}
if(canGet) {
map.put(i*(heights[0].length)+j, 1);
}
430. 扁平化多级双向链表(R) ⭐⭐

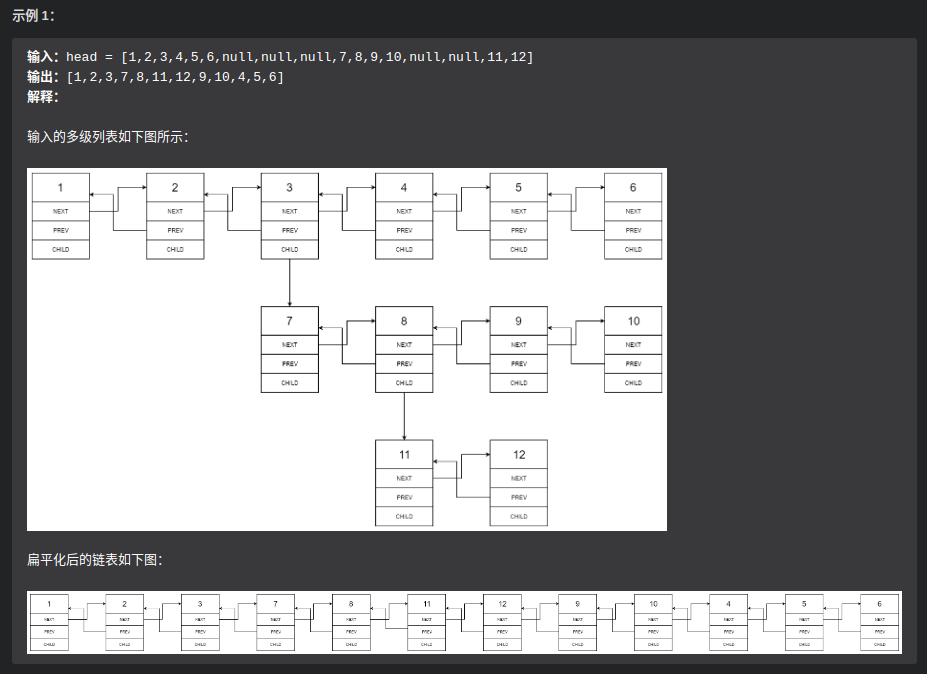
审题
- DFS?
1. 回溯法(×)
Node pre = head;
Node result = pre;
Node mid = head;
Queue<Node> queue = new LinkedList<>();
boolean isJump = false;
while(true) {
if(mid == null) {
Node pullNode = queue.poll();
if(pullNode == null ){
break;
}
isJump = true;
mid = pullNode;
}
if(mid.child != null && !isJump) {
queue.offer(mid);
pre.next = mid.child;
mid = mid.child;
}
else if(mid.next != null) {
pre.next = mid.next;
mid = mid.next;
}
else{
mid = null;
continue;
}
pre = pre.next;
isJump = false;
}
return result;
}
这里没有做出来,想法和回溯是一样的,不过在压栈的考虑上,对对象引用十分不熟悉。。导致压了之后还是会改变值
**反思:**java对象引用
2. 回溯法(转)
public Node flatten(Node head) {
Node node = head;
Node prev = null;
Deque<Node> stack = new ArrayDeque<>();
while (node != null || !stack.isEmpty()) {
if (node == null) {
node = stack.pop();
node.prev = prev;
prev.next = node;
}
if (node.child != null) {
if (node.next != null) stack.push(node.next);
node.child.prev = node;
node.next = node.child;
node.child = null;
}
prev = node;
node = node.next;
}
return head;
}
3. DFS(转)
public Node flatten(Node head) {
dfs(head);
return head;
}
public Node dfs(Node node) {
Node cur = node;
// 记录链表的最后一个节点
Node last = null;
while (cur != null) {
Node next = cur.next;
// 如果有子节点,那么首先处理子节点
if (cur.child != null) {
Node childLast = dfs(cur.child);
next = cur.next;
// 将 node 与 child 相连
cur.next = cur.child;
cur.child.prev = cur;
// 如果 next 不为空,就将 last 与 next 相连
if (next != null) {
childLast.next = next;
next.prev = childLast;
}
// 将 child 置为空
cur.child = null;
last = childLast;
} else {
last = cur;
}
cur = next;
}
return last;
}
437. 路径总和 (I R) ⭐⭐

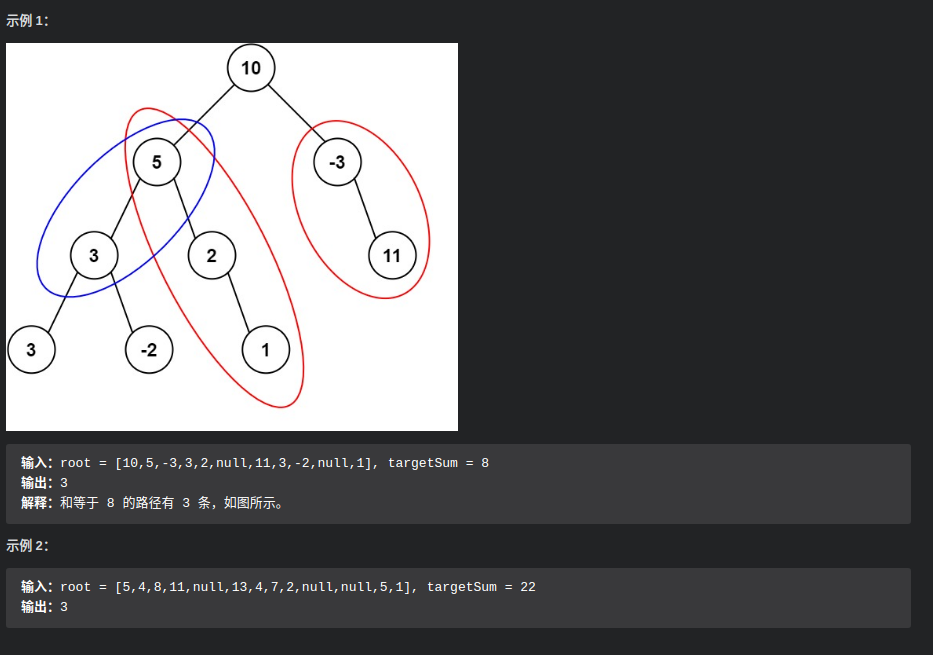
审题
- 二叉树,没有的节点用null表示
- 同一个节点可以有多个组合
- 包含负数
- 路径必须是向下!左右子节点不限
- 首先要确定遍历方式,中序遍历。
- 如何保存某个节点的递加值?dp?
- 以某个节点开始很重要。以某个节点结束不重要。确定遍历方式
1. 递归(x)
int res = 0;
public int pathSum(TreeNode root, int targetSum) {
TreeNode node = root;
if(node != null) {
pathSum(node.left, targetSum);
System.out.println("Parent node : " +node.val);
isNodeEqualNum(node,targetSum);
pathSum(node.right, targetSum);
}
return res;
}
int isNodeEqualNum(TreeNode node, int targetSum) {
if(node == null) {
return 0;
}
int onLeft = isNodeEqualNum(node.left, targetSum) + node.val;
int onMid = isNodeEqualNum(null,targetSum) +node.val;
int onRight = isNodeEqualNum(node.right, targetSum) + node.val;
System.out.println(" Currentnode: " + node.val + " l m r" + onLeft+" "+onMid+" "+onRight);
if(onLeft == targetSum) {
System.out.println("head left");
res++;
}
if(onRight == targetSum) {
System.out.println("head right");
res++;
}
if(onMid == targetSum) {
System.out.println("head mid");
res++;
}
return node.val;
}
这里有想到类似归并排序的那种分治,但是没有考虑到后续的结果如何叠加,三种情况下如何return 到想要的累加值。始终保留在两层递归,而不是多层......
2. 前缀和(转)
class Solution {
public int pathSum(TreeNode root, int sum) {
// key是前缀和, value是大小为key的前缀和出现的次数
Map<Integer, Integer> prefixSumCount = new HashMap<>();
// 前缀和为0的一条路径
prefixSumCount.put(0, 1);
// 前缀和的递归回溯思路
return recursionPathSum(root, prefixSumCount, sum, 0);
}
/**
* 前缀和的递归回溯思路
* 从当前节点反推到根节点(反推比较好理解,正向其实也只有一条),有且仅有一条路径,因为这是一棵树
* 如果此前有和为currSum-target,而当前的和又为currSum,两者的差就肯定为target了
* 所以前缀和对于当前路径来说是唯一的,当前记录的前缀和,在回溯结束,回到本层时去除,保证其不影响其他分支的结果
* @param node 树节点
* @param prefixSumCount 前缀和Map
* @param target 目标值
* @param currSum 当前路径和
* @return 满足题意的解
*/
private int recursionPathSum(TreeNode node, Map<Integer, Integer> prefixSumCount, int target, int currSum) {
// 1.递归终止条件
if (node == null) {
return 0;
}
// 2.本层要做的事情
int res = 0;
// 当前路径上的和
currSum += node.val;
//---核心代码
// 看看root到当前节点这条路上是否存在节点前缀和加target为currSum的路径
// 当前节点->root节点反推,有且仅有一条路径,如果此前有和为currSum-target,而当前的和又为currSum,两者的差就肯定为target了
// currSum-target相当于找路径的起点,起点的sum+target=currSum,当前点到起点的距离就是target
res += prefixSumCount.getOrDefault(currSum - target, 0);
// 更新路径上当前节点前缀和的个数
prefixSumCount.put(currSum, prefixSumCount.getOrDefault(currSum, 0) + 1);
//---核心代码
// 3.进入下一层
res += recursionPathSum(node.left, prefixSumCount, target, currSum);
res += recursionPathSum(node.right, prefixSumCount, target, currSum);
// 4.回到本层,恢复状态,去除当前节点的前缀和数量
// 这里这一步非常重要!避免由于Map中始终保留该路径的值而重复计算
prefixSumCount.put(currSum, prefixSumCount.get(currSum) - 1);
return res;
}
}
// 作者:burning-summer
// 链接:https://leetcode-cn.com/problems/path-sum-iii/solution/qian-zhui-he-di-gui-hui-su-by-shi-huo-de-xia-tian/
学习到这里的一种前缀和思想,可以用Map(cur - target)这种方式来解决,类似之前看到的快速在1 - 100 找到与一个数 相加 == 100的数,而且如何清退掉之前存储的数、如何选择递归顺序、如何递归累加结果,这是需要重新思考的
3. DFS (转)
class Solution {
public int pathSum(TreeNode root, int targetSum) {
if (root == null) {
return 0;
}
// 这个形式非常重要!!!
int ret = rootSum(root, targetSum);
ret += pathSum(root.left, targetSum);
ret += pathSum(root.right, targetSum);
return ret;
}
public int rootSum(TreeNode root, int targetSum) {
int ret = 0;
if (root == null) {
return 0;
}
int val = root.val;
// ①
if (val == targetSum) {
ret++;
}
// 解决递归解决不了当前前缀和的问题 targetSum - val,然后在①中去判断
// 这一步很巧妙
ret += rootSum(root.left, targetSum - val);
ret += rootSum(root.right, targetSum - val);
return ret;
}
}
为什么会比前缀和慢这么多? O(N2)的时间复杂度(全体遍历 + 对每个节点作为父节点的遍历)

这才是我想要的方法的正解,归并排序没有搞清楚。node 、left、right的对应函数调用关系混乱了,区分一下。
这里如何得到在递归中前缀和的值也需要关注。
440. 字典序的第K小的数字 ⭐⭐⭐
Time : 2022 / 3 / 23 22:07
TAG:
审题
- 注意是字典序的排序,并且是1 - n 的数字。
- 特殊点:12345,则有1 10 11 12....100 ... 1000 ... 10000 ... 12345
- 思路:
- 直接:
- 根据n的大小判断,先看数量级。根据具体数量级
- 数量级
- 在
- 根据n的大小判断,先看数量级。根据具体数量级
- 直接:
尝试失败.......
447. 回旋镖的数量 ⭐⭐
审题
- 距离相等
- 考虑顺序
- j、k不等,则必有两种可能
- 可能是数学公式?
- 动态规划?On*n复杂度?
自己想的二位数组存储每个点对应其他点的值,然后查看二位数组中每行数组相同值有几个,通过排列组合做。
没做出来。。。。。。
枚举+哈希表(转)
public int numberOfBoomerangs(int[][] points) {
int ans = 0;
for (int[] p : points) {
Map<Integer, Integer> cnt = new HashMap<Integer, Integer>();
for (int[] q : points) {
int dis = (p[0] - q[0]) * (p[0] - q[0]) + (p[1] - q[1]) * (p[1] - q[1]);
cnt.put(dis, cnt.getOrDefault(dis, 0) + 1);
}
for (Map.Entry<Integer, Integer> entry : cnt.entrySet()) {
int m = entry.getValue();
ans += m * (m - 1);
}
}
return ans;
}
没想到最终最初来居然是自己最开始想的思路。。。。嫌弃HashMap太慢自己用数组散列,结果屁没做出来。。裂开
没做出来:
- 因为这里重复考虑时自己没想清楚,有m个点到第i个点相等。
- 排列组合数学公式有问题
以后还是先考虑做出来,再想优化!!!!
public int numberOfBoomerangs(int[][] points) {
int total = 0;
if(points.length == 1) {
return 0;
}
long[][] res = new long[points.length][points.length + 1];
for(int i = 0; i < points.length; i++) {
long max = 0;
for(int k = 0; k < points.length;k++) {
long temp = getPointsDistance(points[i],points[k]);
max = max>temp? max:temp;
res[i][k] = temp;
}
res[i][points.length] = max;
}
for(int i = 0; i < points.length ; i++) {
int column = (int)res[i][points.length];
long max[] = new long[column+1];
for(int k = 0; k < points.length;k++) {
max[(int) res[i][k]]++;
}
for(int k = 0; k < max.length; k++) {
if(max[k] > 1) {
total += getSequenceCompose((int) max[k])*2;
}
}
}
return total;
}
public long getPointsDistance(int[] one, int[] two) {
long res = (Math.abs((one[0]-two[0])*(one[0]-two[0]) + (one[1]-two[1])* (one[1]-two[1])));
return res;
}
public int getSequenceCompose(int num) {
return reveseMutiple(num)/(reveseMutiple(2) * reveseMutiple(num-2));
}
public int reveseMutiple(int n){
int total = 1;
for(int i = n;i>0;i--){
total *= i;
}
return total;
}
自己修了下之前写的代码,最后结果应该是正确的,但内存消耗太大了,导致超出了内存限制............Shit!
534. 通过删除字母匹配到字典里最长单词 ⭐⭐
审题
- 可通过删除s中的某些字符
- 答案不止一个,则返回长度最长且字典序最小的字符串
1. 暴力迭代+双指针
简单迭代法,比较笨。
public String findLongestWord(String s, List<String> dictionary) {
List<String> result = new ArrayList<>();
for(String str:dictionary) {
int sIndex = 0 ;
int dIndex = 0;
while(sIndex < s.length() && dIndex < str.length()) {
if(s.charAt(sIndex) == str.charAt(dIndex)){
dIndex++;
}
sIndex++;
}
if(dIndex == str.length()) {
result.add(str);
}
}
if(result.size() <= 0 ) {
return "";
}
String maxStr = "";
for(String str:result) {
if(str.length() > maxStr.length()) {
maxStr = str;
}
if(str.length() == maxStr.length()) {
if(judgeStrSeq(str,maxStr) == 1){
maxStr = str;
}
}
}
return maxStr;
}
// 比较字符串的字典序,这里用compareTo就行
public int judgeStrSeq(String o,String a){
for(int i = 0; i < o.length(); i ++) {
if(o.charAt(i) < a.charAt(i)) {
return 1;
}
if(o.charAt(i) > a.charAt(i)) {
return 0;
}
}
return 0;
}
优化,这里可以不要数组,直接一个maxStr作为比较对象。
时间复杂度:O(d×(m+n)),其中 dd 表示 dictionary 的长度,m表示 s 的长度,n 表示 dictionary 中字符串的平均长度。我们需要遍历}dictionary 中的 d 个字符串,每个字符串需要 O(n+m) 的时间复杂度来判断该字符串是否为 s 的子序列。
2. 排序(转)
有 想到这个方法,先排序,长度从长到短顺序来筛选,更容易删选到结果,这里不清楚如何对一个数组进行自定义排序了
// 内部其实是归并排序
Collections.sort(dictionary, new Comparator<String>() {
public int compare(String word1, String word2) {
if (word1.length() != word2.length()) {
return word2.length() - word1.length();
} else {
return word1.compareTo(word2);
}
}
});
时间复杂度:O*(d×m×logd+d×(m+n))
3. 动态规划
考虑前面的双指针的做法,我们注意到我们有大量的时间用于在 s中找到下一个匹配字符。
这样我们通过预处理,得到:对于 s 的每一个位置,从该位置开始往后每一个字符第一次出现的位置

public String findLongestWord(String s, List<String> dictionary) {
int m = s.length();
int[][] f = new int[m + 1][26];
Arrays.fill(f[m], m);
for (int i = m - 1; i >= 0; --i) {
for (int j = 0; j < 26; ++j) {
if (s.charAt(i) == (char) ('a' + j)) {
f[i][j] = i;
} else {
f[i][j] = f[i + 1][j];
}
}
}
String res = "";
for (String t : dictionary) {
boolean match = true;
int j = 0;
for (int i = 0; i < t.length(); ++i) {
if (f[j][t.charAt(i) - 'a'] == m) {
match = false;
break;
}
j = f[j][t.charAt(i) - 'a'] + 1;
}
if (match) {
if (t.length() > res.length() || (t.length() == res.length() && t.compareTo(res) < 0)) {
res = t;
}
}
}
return res;
}
这种方法似乎网传叫 序列自动机,用于子序列匹配。
只能说是牛皮它妈给牛皮开门,牛皮到家了。还是注意这里的主要思路看,大部分时间都花在查找s的字符匹配情况上了,那这里通过预处理,把s的所有情况列出来(最多也就length*26的二维数组)。后面判断则通过O(1)的时间复杂度去对比 耗费O(d x max(str.length))

518. 零钱兑换II ⭐⭐
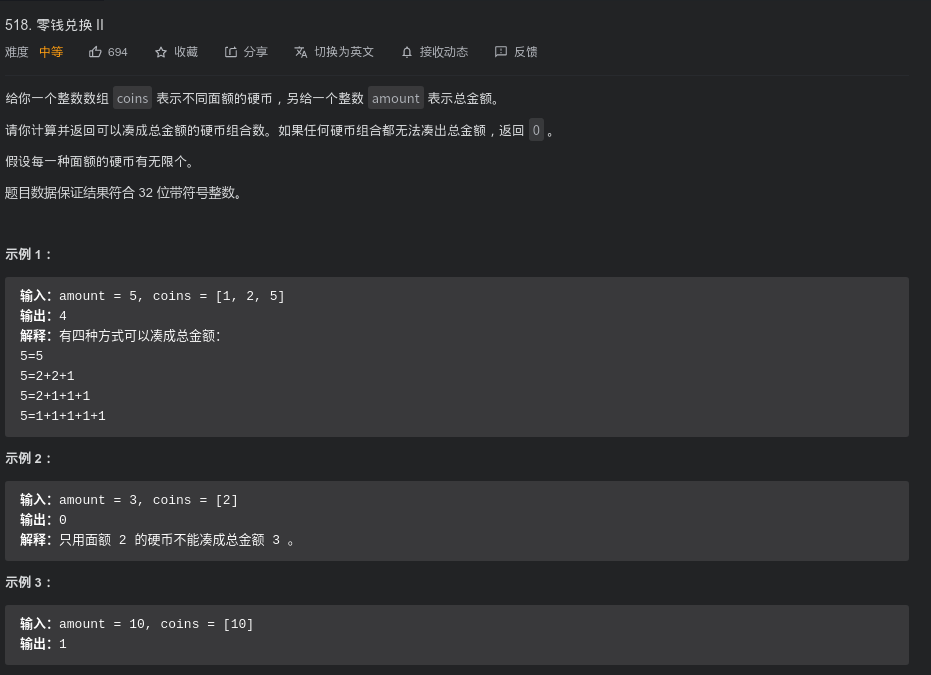
审题
- 每种面额的硬币数目无限
- 可能的做法:动态规划?DFS?
1. 链表实现的DFS (超时)
链表实现的DFS,能够到达底层就为总数加1,而且这里最开始犯了一个错误:
这里题目的意思是不区分1+2+2和2+2+1,后面想了一下,只要把这里新建Node的数据val,改成父节点的val,就能够实现从大到小的排除,而不用大费周章的改算法。
class Solution {
public int change(int amount, int[] coins) {
Node temp;
int total = 0;
int min = coins[0];
int max = coins[coins.length - 1];
int curIndex = coins.length - 1;
Node head = new Node(amount,curIndex,0);
while(head != null) {
if(head.val < 0) {
while(head.father!= null && head.father.val < 0) {
head = head.father;
}
head = head.father;
if(head != null) {
head.val--;
}
continue;
}
if(head.res == 0){
total += 1;
head = head.father;
if(head != null) {
head.val--;
}
continue;
}
if(head.res - coins[head.val] < 0){
head.val--;
continue;
}
temp = new Node(head.res - coins[head.val], head.val, 0);
temp.father = head;
head = temp;
}
return total;
}
}
class Node{
int res;
int val;
int cnt;
Node father;
Node(int res, int val, int cnt) {
this.res = res;
this.val = val;
this.cnt = cnt;
}
}
2. 数组实现的DFS (超时)
以为换用数组来时间会更快,没想到测了一下时间,两者相差无几,看来问题还是出在DFS上而不在于具体的实现方式
public int change(int amount, int[] coins) {
int total = 0;
if(amount == 0)
return 1;
int[] arr = new int[amount + 1];
int[] arrIndex = new int[amount + 1];
int i , j;
i = j = 1;
arr[0] = amount;
arrIndex[0] = coins.length - 1;
while(arrIndex[0] >= 0) {
if(arrIndex[j - 1] < 0) {
while(j > 0 && arrIndex[j - 1] < 0){
j--;
i--;
}
arrIndex[j-1]--;
continue;
}
if(arr[i - 1] == 0) {
total += 1;
i--;j--;
if(j > 0) {
arrIndex[j-1]--;
}
continue;
}
if(arr[i - 1] - coins[arrIndex[j - 1]] < 0) {
arrIndex[j - 1]--;
continue;
}
arr[i] = arr[i - 1] - coins[arrIndex[j - 1]];
arrIndex[j] = arrIndex[j - 1];
i++;
j++;
}
return total;
}
3. 完全背包(转)
3.1 二维
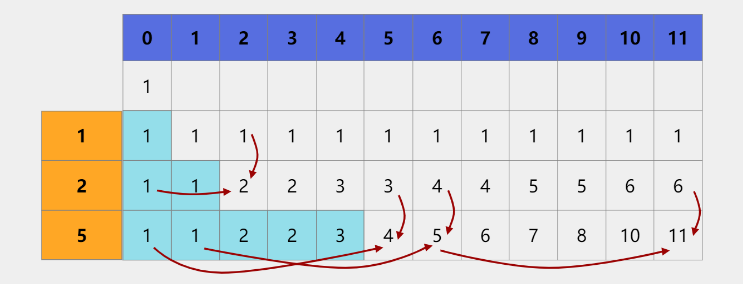
加入一枚新的硬币后,可以有以下两种可能:
- 要么是不要这枚硬币的组合
- 要么是加一枚这枚硬币的组合
⏺️ 这里我有考虑到比如6块钱需要3枚2块硬币来组成,只加一枚那就会遗漏数目。但其实不会,因为它是叠加的过程,6块钱其实由2块钱而来,所以肯定会包含进去的
class Solution {
public int change(int amount, int[] coins) {
int [][] dp = new int[coins.length+1][amount+1];
dp[0][0] = 1;
for (int row = 1; row <= coins.length; row++) {
for (int col = 0; col <= amount; col++) {
dp[row][col] = dp[row-1][col] + (col>=coins[row-1]?dp[row][col-coins[row-1]]:0);
}
}
return dp[coins.length][amount];
}
}
O(amount * coins.length)的空间复杂度
O(amount * coins.length)的时间复杂度
3.2 一维优化
特点:值都由之前的值决定
class Solution {
public int change(int amount, int[] coins) {
int []dp = new int[amount+1];
dp[0] = 1;
for (int coin : coins) {
for (int i = coin; i <= amount; i++) {
dp[i] += dp[i-coin];
}
}
return dp[amount];
}
}
// 作者:cheungq-6
// 链接:https://leetcode-cn.com/problems/coin-change-2/solution/hua-tu-li-jie-cong-chang-gui-er-wei-dpda-4gfy/
总结
自己总算是了确了DFS的执念了,之前一想到啥就容易想到DFS,但确实这类题的背包特点太明显了,自己对背包问题还是不熟悉,最开始想的也是从amount 1-n的迭代,但没想清楚如何用规划来迭代的算
- 背包问题先从朴素方法解决,然后再优化到一维
539. 最小时间差 ⭐⭐
审题
- 最小时间差,正数,还必须用分钟数表示
- 难点:一个数组中的按一定规则相差最小的数,暴力法肯定是On^2的时间复杂度(针对每一个数,找到它的相差的最小数再依次比较)
- 可能的做法:双指针?排序后再做?
1. 暴力法
二次循环,On^2的时间复杂度,O1的空间复杂度
2. 排序后依次比较
先转化成可排的数组,Onlogn排序后依次比较差值,Onlogn的时间复杂度 On的空间复杂度(但在字符串的时间形式的数组转化可能耗费时间)
注意的就是不同区间的比较,有以下情况:
- 00:00 , 23:59
- 00:00 11:59
这两种情况是需要分别讨论的,这里用Math.min去判断
优化
不需要,因为这里比较前一个的差值,最后再算最后一个与第一个的差值就行了,所以我这里看了三种情况(实际只应该有两种),进行了三次最小值判断(实际不应该有)
public int findMinDifference(List<String> timePoints) {
int[] timeMinute = new int[timePoints.size()];
int min = Integer.MAX_VALUE;
int A_DAY = 24* 60;
for(int i = 0; i <timePoints.size(); i++) {
int hour = Integer.parseInt(timePoints.get(i).substring(0,2));
int minute = Integer.parseInt(timePoints.get(i).substring(3,5));
timeMinute[i] = hour*60 +minute;
}
Arrays.sort(timeMinute);
int temp;
for(int i = 0; i <timeMinute.length; i++) {
if(i == 0) {
temp = Math.min(Math.min(timeMinute[i+1]-timeMinute[i], A_DAY - timeMinute[i + 1] + timeMinute[i]), Math.min(timeMinute[timeMinute.length - 1]-timeMinute[i], A_DAY - timeMinute[timeMinute.length - 1] + timeMinute[i]));
}else if(i == timeMinute.length - 1) {
temp = Math.min(Math.min(timeMinute[i]-timeMinute[0], A_DAY - timeMinute[i] + timeMinute[0]), Math.min(timeMinute[i]-timeMinute[i - 1], A_DAY - timeMinute[i] + timeMinute[i - 1]));
}
else{
temp = Math.min(Math.min(timeMinute[i+1]-timeMinute[i], A_DAY - timeMinute[i + 1] + timeMinute[i]), Math.min(timeMinute[i]-timeMinute[i - 1], A_DAY - timeMinute[i] + timeMinute[i - 1]));
}
if(min > temp)
min = temp;
}
return min;
}
意外居然一次过 😦
空间复杂度On慢一点可以理解(但这里也可以优化成O1的空间复杂度,直接在原List中解决 排序占用LogN的栈空间!!!),但因为OnLogn的时间复杂度所以只有70%,并且也不需要两次判断。 所以这题肯定是有LogN 的时间复杂度的解法滴
好吧,后来看了一下,我这个算法前面加个
if(timePoints.size() > 24 * 60) {
return 0;
}
也是这个 .......
3. 鸽巢原理(抽屉原理) (转)
主要解决的是当N很大时,会有许多重复的时间(值得注意,加个判断就能解决上限问题),按照第二种方法的会有浪费的空间,能够将空间复杂度压缩到Log(min(N,60*24))
class Solution {
public int findMinDifference(List<String> timePoints) {
int n = timePoints.size();
if (n > 1440) {
return 0;
}
Collections.sort(timePoints);
int ans = Integer.MAX_VALUE;
int t0Minutes = getMinutes(timePoints.get(0));
int preMinutes = t0Minutes;
for (int i = 1; i < n; ++i) {
int minutes = getMinutes(timePoints.get(i));
ans = Math.min(ans, minutes - preMinutes); // 相邻时间的时间差
preMinutes = minutes;
}
ans = Math.min(ans, t0Minutes + 1440 - preMinutes); // 首尾时间的时间差
return ans;
}
public int getMinutes(String t) {
return ((t.charAt(0) - '0') * 10 + (t.charAt(1) - '0')) * 60 + (t.charAt(3) - '0') * 10 + (t.charAt(4) - '0');
}
}
// 链接:https://leetcode-cn.com/problems/minimum-time-difference/solution/zui-xiao-shi-jian-chai-by-leetcode-solut-xolj/
4. 优化 - 排序+鸽巢 (转)
前面第三题虽然用了字符串排序,但我猜这里字符串排序的时间还是慢于数字排序的,所以也是这里快一点的原因吧
后面看了一下,除了鸽巢原理基本上与第二种方法思路上相差无几(当然我的更笨一点)😓
class Solution {
public int findMinDifference(List<String> timePoints) {
if (timePoints.size() > 1440) {
return 0;
}
int[] cache = new int[timePoints.size()];
for (int i = 0; i < cache.length; i++) {
String timePoint = timePoints.get(i);
cache[i] = Integer.parseInt(timePoint.substring(0, 2)) * 60 + Integer.parseInt(timePoint.substring(3));
}
Arrays.sort(cache);
int min = Integer.MAX_VALUE;
for (int i = 1; i < cache.length; i++) {
min = Math.min(min, cache[i] - cache[i - 1]);
}
return Math.min(min, cache[0] + 1440 - cache[cache.length - 1]);
}
}
// 作者:kyushu
// 链接:https://leetcode-cn.com/problems/minimum-time-difference/solution/rustgolangjava-pai-xu-ge-chao-li-lun-by-kt9yd/
我只能说,精彩......
总结
- 碰到字符串或数字都可排序的情况,先考虑数字排序,因为可能更快
- 不要那些不必要的运算,想清楚....
- 考虑抽屉原理 差值要考虑N非常大的时候对N的限制,加if() return 的限制条件有时候有奇效!
589. N叉树的前序遍历 ⭐
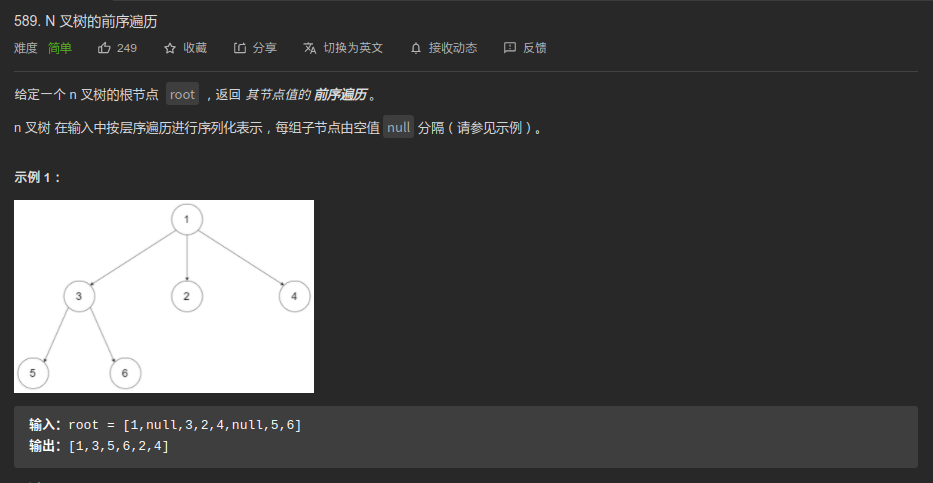
审题
前序遍历的概念
可能的算法:队列 栈
做前思路:
- 简单:按照左儿子的深层遍历 递归
1. 迭代
class Solution {
public List<Integer> preorder(Node root) {
List<Integer> res = new ArrayList<>();
Node cur = root;
Node left,right;
innerMethod(cur,res);
return res;
}
void innerMethod (Node node, List<Integer> res) {
if(node == null)
return ;
res.add(node.val);
// 重点主要在这一段话了
for(int i = 0; i < node.children.size(); i++) {
if(node.children.get(i) != null) {
innerMethod(node.children.get(i),res);
}
}
}
}
不错子,还是比较快想出来了。觉得迭代没有递归来得快,就递归了一下
反思
- 最开始把条件看错了,以为是二叉树....
- 附一篇解决各种树 各种顺序遍历的问题总结 Link~~ ~~
599. 两个列表的最小索引总和 ⭐
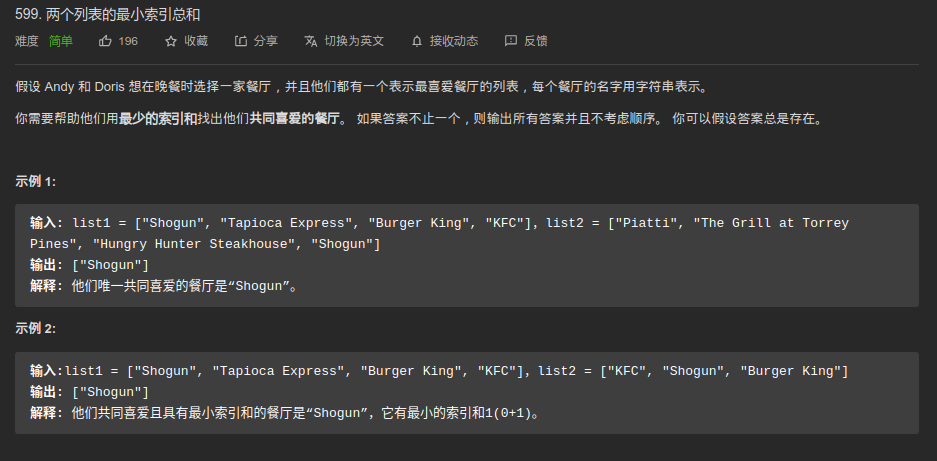
审题
- 两个字符串数组中找相同的字符串,且索引和最小。输出所有可能答案
- 思路:
- 简单:O(m) * O(n) 的时间复杂度,两层遍历(实际超过界限值就可以直接输出答案)
- 进阶:能否在O(m + n)即一次遍历后求出?
1. 双层循环
暴力解法,找到最小值,然后再循环一次找索引和等于最小值的那些字符串
部分优化(空间复杂度提升10%):
- List 去掉,换成记录数组长度的int
- 通过i + j > minSum && minSum != -1删除冗余的判断操作
public String[] findRestaurant(String[] list1, String[] list2) {
int minSum = -1;
List<String> res = new ArrayList<>();
for(int i = 0 ; i < list1.length; i++) {
for(int j = 0; j < list2.length; j++) {
if(list1[i].equals(list2[j])) {
if(minSum == -1) {
minSum = i + j;
}else if(i + j < minSum) {
minSum = i + j;
}
}
else if(i + j >= minSum && minSum != -1) {
break;
}
}
}
for(int i = 0 ; i < list1.length; i++) {
for(int j = 0; i + j <= minSum && j < list2.length; j++) {
if(i + j == minSum && list1[i].equals(list2[j])) {
res.add(list1[i]);
}
}
}
String[] ans = new String[res.size()];
for(int i = 0 ; i < res.size(); i++) {
ans[i] = res.get(i);
}
return ans;
}
2. 双指针
两个index同步增加,已达到这一时刻总是最小索引和的情况。
public String[] findRestaurant(String[] list1, String[] list2) {
int i = 0;
int j = 0;
int minSum = -1;
int count = 0;
String[] ans ;
while(count == 0) {
minSum++;
i = 0;
j = minSum;
// 避免溢出情况
if(minSum >= list2.length) {
j = list2.length - 1;
i = minSum - j;
}
count = 0;
while(j >= 0 && i < list1.length ) {
if(list1[i++].equals(list2[j--]))
count ++;
}
}
ans = new String[count];
int index = 0;
for(i = 0; i <= minSum && i < list1.length; i++) {
if(minSum - i >= list2.length) {
continue;
}
if(list1[i].equals(list2[minSum-i])) {
ans[index++] = list1[i];
}
}
return ans;
}
感觉是最优的路线了,但复杂度还是偏高啊,理论上是O(m)*O(n)的时间复杂度
3. 哈希缓存
思路还是来自能否在O(m + n)的时间复杂度内找到想要的值,先放一个数组元素过去,然后在哈希判断第二个数组中每个元素值是否在哈希表中存在,存在则说明相等,则增加其哈希值,(并与当前最小记录索引和比较)。集合用来进行当前最小索引和元素的清空和增加
public String[] findRestaurant(String[] list1, String[] list2) {
int curMin = -1;
HashMap<String, Integer> map = new HashMap<>();
List<String> list = new ArrayList<>();
for(int i = 0; i < list1.length; i++) {
map.put(list1[i], i);
}
for(int i = 0; i < list2.length; i++) {
Integer index = map.get(list2[i]);
if(index != null) {
map.put(list2[i], index + i);
if(curMin == -1) {
curMin = index + i;
list.add(list2[i]);
}
else if(curMin > index + i) {
curMin = index + i;
list.clear();
list.add(list2[i]);
}else if(curMin == index+i) {
list.add(list2[i]);
}
}
}
String[] ans = new String[list.size()];
for(int i = 0 ; i < list.size(); i++) {
ans[i] = list.get(i);
}
return ans;
}
}
时间复杂度低 O(m + n)
空间复杂度高 O(m + n),且大量字符串占据
优化
简单的一句 足矣.....(在第二个集合判断之前插入判断,避免了之后的无用元素判断)
// ...
for(int i = 0; i < list2.length; i++) {
if(curMin != -1 && i > curMin) break; // inserted
Integer index = map.get(list2[i]);
// ...
反思
- 思路还算清晰,但是最开始没有想到O(n)的解决方法。以后解决问题 在优化思路上一定要先想到一次遍历就解决问题的方法,不要缠在多重嵌套中
- 优化方式注意:确保思路最优再考虑优化。有些优化看起来还不错,但涉及到最坏情况下,还是是不好的,是治标不治本的方法,考虑清楚是否划算再优化,不行就重新换思路。
- 对一些最小值 最大值的搜索问题,索引上优化时就可以进行临界判断,此后大于(或小于)这个值的都不要.....
639. 解码方法 ⭐⭐⭐
审题
- 6与06不同
- ‘‘*’’字符不表示0
- 队列?递归
1. 递归(超时)
public int numDecodings(String s) {
char[] chars = s.toCharArray();
int res= getNum(chars,0);
return res;
}
int getNum(char[] chars, int i){
if(i == 0 && chars[i] == '0'){
return 0;
}
if(i >= chars.length - 1){
return 1;
}
// two option
if(chars[i] == '1' || (chars[i] == '2' && chars[i+1] <= '6')) {
if(chars[i+1] == '0') {
return getNum(chars,i+2);
}
return getNum(chars,i+2) + getNum(chars,i+1);
}
else{
if(chars[i] == '0'){
return 0;
}
// only one option
return getNum(chars,i+1);
}
}
超时......
测试后,答案正确,但耗时太长
2. dp(转)
public int numDecodings(String s) {
int n = s.length();
int[] f = new int[n + 1];
f[0] = 1;
for (int i = 1; i <= n; ++i) {
if (s.charAt(i - 1) != '0') {
f[i] += f[i - 1];
}
if (i > 1 && s.charAt(i - 2) != '0' && ((s.charAt(i - 2) - '0') * 10 + (s.charAt(i - 1) - '0') <= 26)) {
f[i] += f[i - 2];
}
}
return f[n];
}
// 优化后
public int numDecodings(String s) {
int n = s.length();
// a = f[i-2], b = f[i-1], c=f[i]
int a = 0, b = 1, c = 0;
for (int i = 1; i <= n; ++i) {
c = 0;
if (s.charAt(i - 1) != '0') {
c += b;
}
if (i > 1 && s.charAt(i - 2) != '0' && ((s.charAt(i - 2) - '0') * 10 + (s.charAt(i - 1) - '0') <= 26)) {
c += a;
}
a = b;
b = c;
}
return c;
}
这里之前一直在想递归和迭代.....有想过动态规划,但没规划出来........
动态规划和递归的耗时
dp做这道题 基本秒出,递归则需要7s左右,由此dp的重要性。
以后遇上递归超时的问题,要多考虑一下动态规划。。。。。看看能否以函数表达式去表示f(x),进而使用dp解。
653. 两数之和IV-输入BST ⭐
Time : 2022 / 3 / 21 21 : 25
TAG : DFS \ BFS \ Hash \ InOrder Traversal
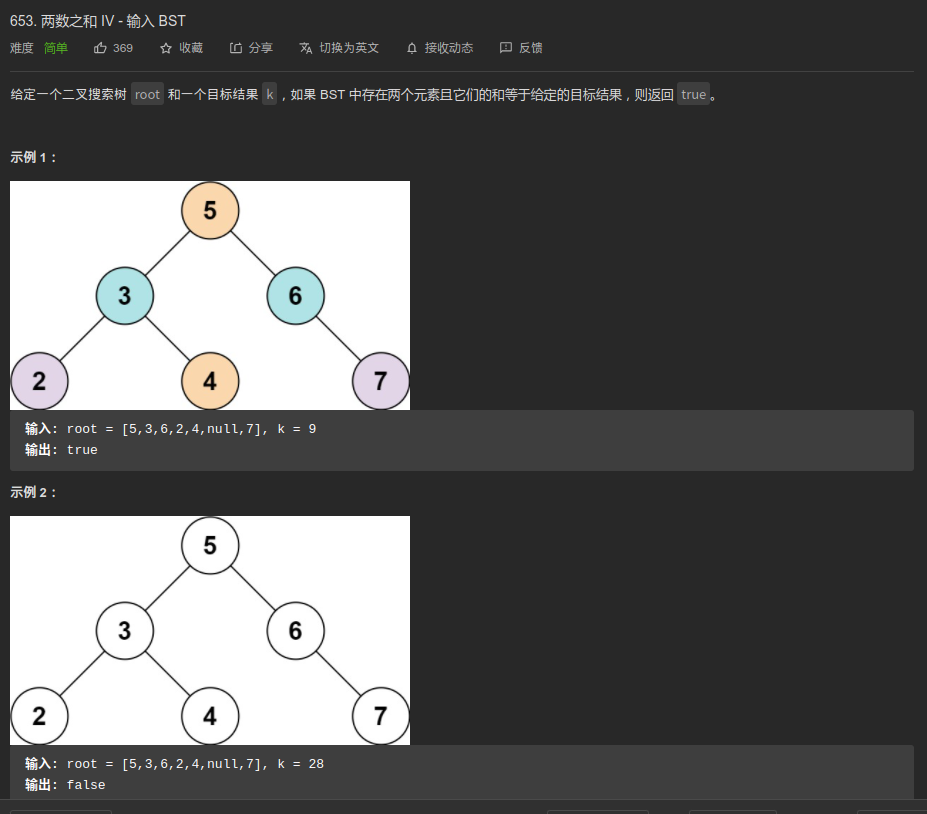
审题
- 看
- 思路:
- 简单:
- 对每个小于k的元素,找到a,找到等于k-a的元素
- 当然也可以一次遍历读出来,然后存到Hash表中,然后再找x-a,但这样就没意义了
- 简单:
1. 前序搜索DFS
先说总体思路:
- 当前元素curNode.val是否比k小,如果小,则去找k-curNode.val是否在二叉搜索树中;
- 先找left,整体是中序遍历
- left找不到,找right
- 还找不到,寄
- 比k大,则找left,直到比k小,找不到这样的数,寄
public boolean findTarget(TreeNode root, int k) {
TreeNode curNode = root;
// Optimize: find lowest level that val < k
while(curNode != null && curNode.val > k) {
if(curNode == null) {
return false;
}
if(curNode.left != null) {
curNode = curNode.left;
}else{
break;
}
}
return preResearch(curNode, k, root);
}
public boolean binaryResearch(TreeNode node, int k,TreeNode originNode) {
if(node == null ) {
return false;
}
if(node.val > k) {
return binaryResearch(node.left,k, originNode);
}
if(node.val < k) {
return binaryResearch(node.right,k, originNode);
}
// 1. in case of same val but different node
// 2. in case of relocate to originNode (eg.{1} 2)
if(originNode == node) {
return false;
}
if(node.val == k) {
return true;
}
return false;
}
// Wrong Name, actually to be midSearch...
public boolean preResearch(TreeNode node, int k, TreeNode root) {
boolean left = false;
boolean right = false;
boolean ans = false;
if(node == null) {
return false;
}
else{
ans = binaryResearch(root, k - node.val, node);
}
if(ans){
return true;
}
if(node.left != null) {
left = preResearch(node.left, k, root);
}
if(left) {
return true;
}
if(node.right != null) {
right = preResearch(node.right, k, root);
}
return right;
}
时间复杂度:BST查找元素耗时O(logN) 最坏每个小于k的元素都找一次O((N-a)logN){但具体多少我这里不知道怎么算了,根据答案的结果来看应该是On?},但其实是小于它的
空间复杂度:一个元素有O(N)的栈空间(方法占用)
优化点
优化点
在preResearch中,判断条件,按照中序遍历的条件,哪一个能跑就直接跑,不过之后的是非了
错误的优化点
这里我最开始使用了这样的优化:
while(curNode != null && curNode.val > k) {
if(curNode == null) {
return false;
}
if(curNode.left != null) {
curNode = curNode.left;
}else{
break;
}
}
其实这样想的思路的初衷是错误的,因为我仅仅考虑了为正整数的情况,当为负数时,非要找一个val < k 的数,则会找到更左下方,但其实不影响结果,为什么?因为只要查找k - node.val的数是从root查找的,所以再怎样如果有对应的k-node.val的元素,就会找到,也算是一个小优化
2. DFS + 哈希(转)
这是我说的没太大意思的方法的优化版本(DFS优化)
class Solution {
Set<Integer> set = new HashSet<Integer>();
public boolean findTarget(TreeNode root, int k) {
if (root == null) {
return false;
}
if (set.contains(k - root.val)) {
return true;
}
set.add(root.val);
return findTarget(root.left, k) || findTarget(root.right, k);
}
}
时间复杂度波动较大 40% ~ 90%
3. BFS + 哈希表(转)
具体实现就不写了
4. DFS + 哈希表 + 双指针(转)
比较有意思,先把BST转化成数组,在数组层面上找
具体地,我们使用两个指针分别指向数组的头尾,当两个指针指向的元素之和小于 kk 时,让左指针右移;当两个指针指向的元素之和大于 kk 时,让右指针左移;当两个指针指向的元素之和等于 kk 时,返回 。最终,当左指针和右指针重合时,树上不存在两个和为 kk 的节点,返回 \text{False}False。
原理见:LeetCode 167 两数之和II
反思
- 整体做的不行,整体思路出来快,但查错时间久,被各种null错误卡住,使用val \ left \ right 时没有进行非空判断出问题最多
- 能把中序的递归想出来还不错
655. 输出二叉树⭐⭐
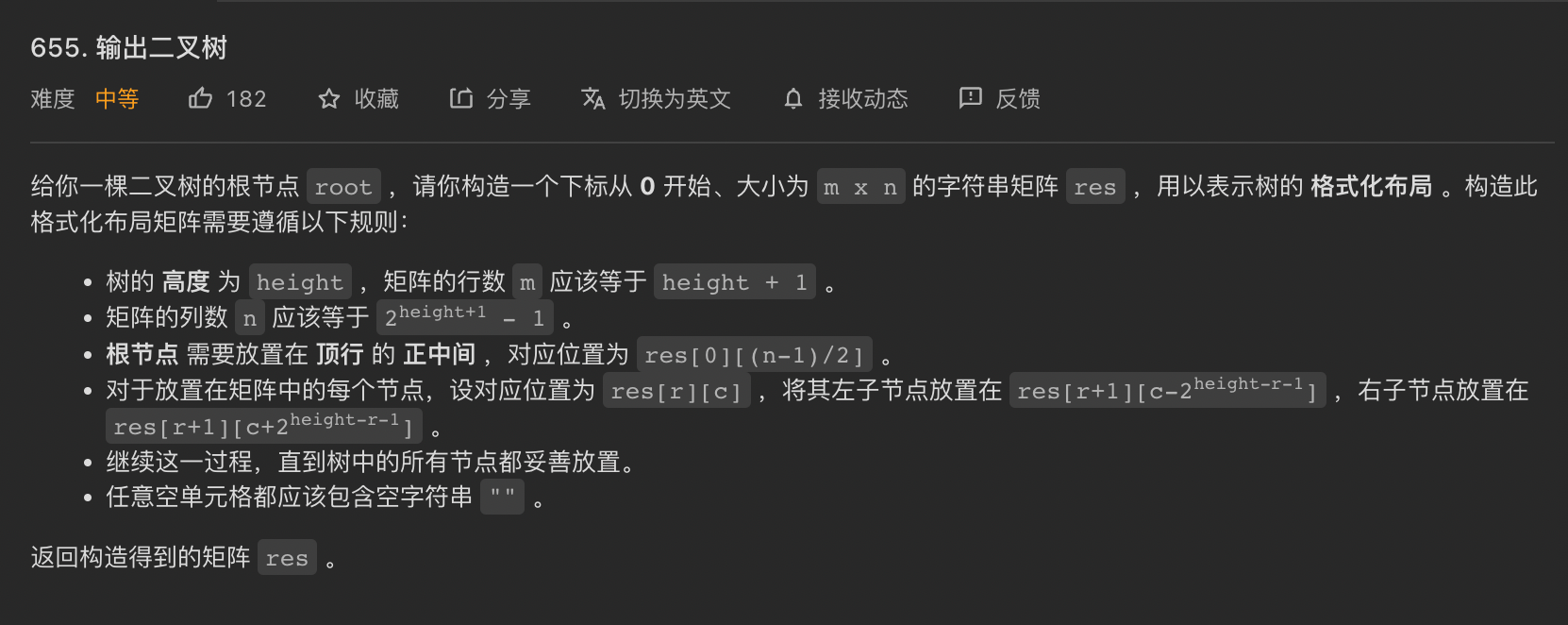
审题
- 转化后矩阵的元素为字符串
- 是否要先确定树的高度从而来确定矩阵r x c的数值;或者在一次遍历的时候动态调整前面的长度
- row = height
- col = 2^(height - 1) + 1
- 思路:
- 遍历树得出高度,再层次遍历填矩阵每一行的值;但这里每一层如何确定其兄弟元素之间的距离?
693. 交替位二进制数 ⭐
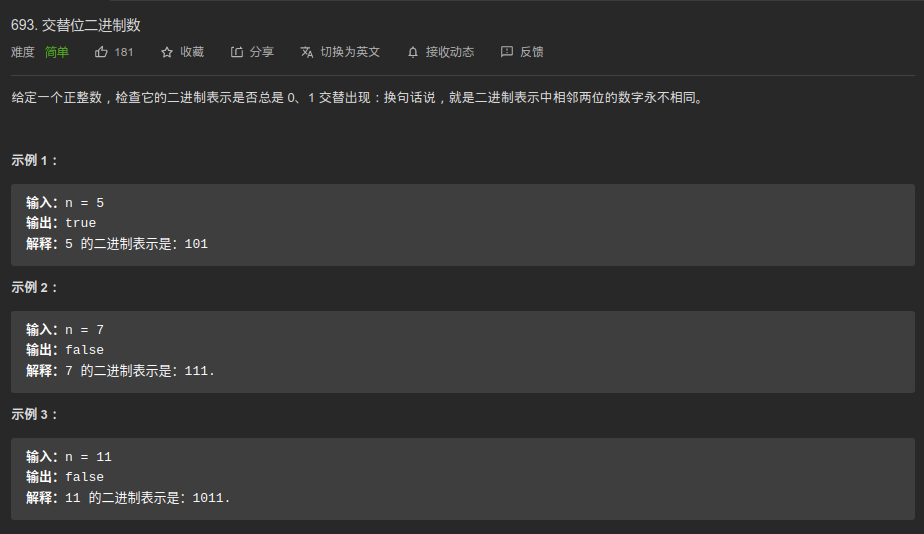
审题
- 有相同数字:
- 1 相邻 2^n + 2 ^ (n -1)
- 0 相邻 同理
- 可能的思路:位运算、左右位移?
- 思路:
- 直接:
- 转换成二进制,一步步比较
- 左右位移
- 进阶:
- 二进制 的位运算
- 直接:
1. 位运算
思路还是比较清楚,关键是判断邻近的位是否重复,而邻近的位的重复情况是2 ^ n 与 2 ^ (n-1)与 这个数的关系,但这种比较可以通过右移并且 并上1 得到最后一位来判断
public boolean hasAlternatingBits(int n) {
int lastBit = n & 1;
int temp = n >> 1;
// temp / 2 == 0则不判断了
while(temp != 0) {
// 如果与前一位相同,则不满足
if(lastBit == (temp & 1)) {
return false;
}
lastBit = temp & 1;
temp = temp >> 1;
}
return true;
}
位运算很快
反思
- & 和 ^ 符号搞错了!!& 是并 ^ 是异或 ~是同或
- 思路不错,想的比较块
704. 二分查找 ⭐

思考
有序 升序 、返回下标
1. 二分查找
public int search(int[] nums, int target) {
int low = 0;
int high = nums.length-1;
int mid = 0;
while(low <= high) {
mid = (low + high) / 2 ;
if(nums[mid] < target) {
low = mid+1;
}
else if(nums[mid] > target) {
high = mid-1;
}
else{
return mid;
}
}
return -1;
}
主要还是二分法的实现,注意while的判别条件 <=
注意low 和 high的增加和减少,避免在 l h target在 1 2 2 情况下的问题
二分法还是有欠缺
720. 词典中最长的单词 ⭐
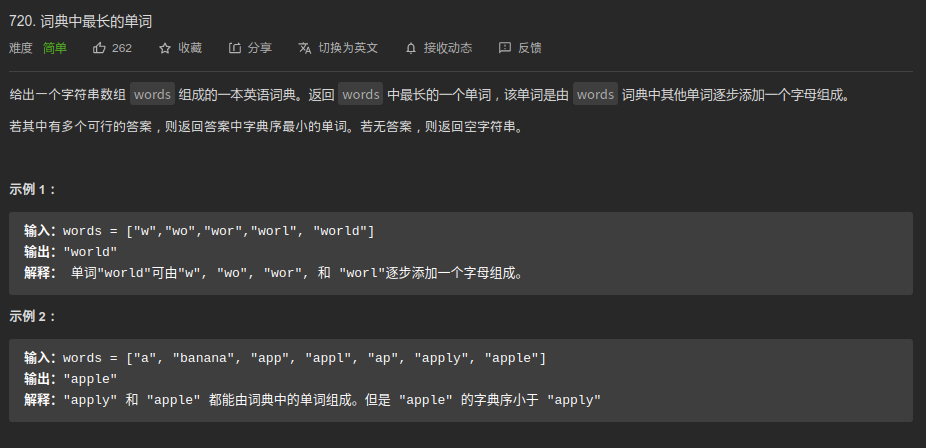
思考
- 该单词又其他单词逐步添加一个字母组成(不是这样的单词就不是正确答案,可能有其他随意的单词 ),不一定是从一个单词开始添加起(吗?),且可能是乱序。 多个答案则返回字典序最小的。
- 细节:一个字母后可以跟不同的字母,跟不同字母后最终长度可能变化。
- 可能的算法/数据结构:DFS?哈希?前缀之类的东西?
- 思路:
- 简单:以某一个一个字母的单词为首,遍历数组,得到一个最终的单词,首字母存在。存在集合中?
- 进阶:老话:能否在On的时间复杂度内求得?
1. 哈希-前缀比较
HashSet作为判断容器。判断条件:
- 首字母没加就加进去
- 这个单词的前n - 1个单词在set中,且这个单词不在set中就添加进去
public String longestWord(String[] words) {
HashSet<String> set = new HashSet<>();
for(int i = 0; i < words.length; i++) {
if(words[i].length() == 1) {
if(!set.contains(words[i])) {
set.add(words[i]);
i = -1;
}
}else{
if(!set.contains(words[i]) && set.contains(words[i].substring(0,words[i].length() - 1))) {
set.add(words[i]);
i = -1;
}
}
}
Iterator<String> it = set.iterator();
String maxWord = "";
while(it.hasNext()) {
String next = it.next();
if(next.length() > maxWord.length()) {
maxWord = next;
}
else if(next.length() == maxWord.length()) {
maxWord = maxWord.compareTo(next) > 0 ? next :maxWord;
}
}
return maxWord;
}
时间复杂度:设有最长单词数a个,单词长度为m,整体数组长度为M。则时间复杂度O(a) * O(m) * O(M),非常高
空间复杂度:O(a * m)
2. 哈希+集合一次遍历
与之前思路相同,不过仅仅是一次遍历后,通过再次遍历每个元素,判断其前缀是否都存在
缺点:存在冗余的判断,比如a ap app 会依次判断
public String longestWord(String[] words) {
HashSet<String> set = new HashSet<>();
ArrayList<String> list = new ArrayList<>();
for(int i = 0; i < words.length; i++) {
set.add(words[i]);
}
for(int i = 0; i < words.length; i++) {
int j = 1;
for(; j <= words[i].length(); j++) {
if(!set.contains(words[i].substring(0,j))) {
break;
}
}
if(j > words[i].length()) {
list.add(words[i]);
}
}
String maxWord = "";
for(String next : list) {
if(next.length() > maxWord.length()) {
maxWord = next;
}
else if(next.length() == maxWord.length()) {
maxWord = maxWord.compareTo(next) > 0 ? next :maxWord;
}
}
return maxWord;
}
时间复杂度:O(a) * O(m)比之前稍微好一点
空间复杂度:O(n)
优化
按字符串长度迭代
一次遍历的思路:关键在于解决之前对每个元素前n-1个前缀都重复判断的冗余操作
核心思路:以数组元素的length为标杆,Set只存当前前length前缀都存在的字符串,按length遍历时,只用判断第length - 1个前缀(substring(0,length-1))的那个字符串是否存在就行,感觉有一点dp的思路吗?
这里还有一个已优化点:如果出现字符串长度断层的现象,例如{"a","ab","abcd"},这样也不会把abcd计入,并且不会再看之后长度的数组了(因为已经**产生断层,**后续字符串肯定不满足题意了)
public String longestWord(String[] words) {
HashSet<String> set = new HashSet<>();
ArrayList<String> list = new ArrayList<>();
for(int i = 0; i < words.length; i++) {
if(words[i].length() == 1) {
set.add(words[i]);
list.add(words[i]);
}
}
int length = 2;
int flag = -1;
for(int i = 0; i < words.length; i++) {
if(words[i].length() == length) {
if(set.contains(words[i].substring(0,length - 1))) {
list.add(words[i]);
set.add(words[i]);
flag = 1;
}
}
if(i == words.length - 1 && flag == 1) {
i = -1;
length++;
flag = -1;
}
}
String maxWord = "";
for(String next : list) {
if(next.length() > maxWord.length()) {
maxWord = next;
}
else if(next.length() == maxWord.length()) {
maxWord = maxWord.compareTo(next) > 0 ? next :maxWord;
}
}
return maxWord;
}
时间复杂度:O(n) * O(length) (length为不断层的最大字符串长度)
空间复杂度:O(n)
官方解答跟我思路一致,但是是Arrays.sort先排序了一下数组,没有用到按层遍历,其实没有做断层方面优化,比 这里差一点,所以时间复杂度在60%
3. 字典树 / 前缀树
解决字符串前缀匹配问题的好帮手!要先清楚其数据结构。抽空了解了一下字典树,非常适合解决此类问题
class Solution {
public String longestWord(String[] words) {
Trie trie = new Trie();
for (String word : words) {
trie.insert(word);
}
String longest = "";
for (String word : words) {
if (trie.search(word)) {
if (word.length() > longest.length() || (word.length() == longest.length() && word.compareTo(longest) < 0)) {
longest = word;
}
}
}
return longest;
}
}
class Trie {
Trie[] children;
boolean isEnd;
public Trie() {
// 最多26个字母
children = new Trie[26];
isEnd = false;
}
public void insert(String word) {
Trie node = this;
for (int i = 0; i < word.length(); i++) {
char ch = word.charAt(i);
int index = ch - 'a';
if (node.children[index] == null) {
node.children[index] = new Trie();
}
node = node.children[index];
}
node.isEnd = true;
}
public boolean search(String word) {
Trie node = this;
for (int i = 0; i < word.length(); i++) {
char ch = word.charAt(i);
int index = ch - 'a';
if (node.children[index] == null || !node.children[index].isEnd) {
return false;
}
node = node.children[index];
}
return node != null && node.isEnd;
}
}
// 作者:LeetCode-Solution
// 链接:https://leetcode-cn.com/problems/longest-word-in-dictionary/solution/ci-dian-zhong-zui-chang-de-dan-ci-by-lee-k5gj/

反思
思考错误:在for(;;)循环时想重新循环,在循环内部使用i = 0 导致出错,没有考虑每次循环后i 还会加1 ,导致实际结果为 1 开始的情况。
脑袋不是很清晰
一次遍历的思想还是能提供主要思路!
for循环重置时i = -1 还是 i = 0 需要注意
未考虑length == 1时 把字符串加进集合中
字符串长度是方法,而不是属性(细节)
compareTo比较字符串的字典序!a.compareTo(b):
< 0说明a的字典序小于b
0 则a的字典序大于b
728. 自除数 ⭐

审题
- 返回的是范围内满足条件的数
- 可能的算法:DP(想法是好的)
- 思路:
- 直接:
- 拆分位数,按十进制除
- 直接:
1. 迭代
public List<Integer> selfDividingNumbers(int left, int right) {
List<Integer> list = new ArrayList<>();
for(int i = left; i <= right; i++) {
if(isSelfDividNum(i)) {
list.add(i);
}
}
return list;
}
public boolean isSelfDividNum(int n) {
int temp = n;
while(temp != 0) {
int div = temp % 10;
temp /= 10;
if(div == 0 || n % div != 0){
return false;
}
}
return true;
}
是真没想到最直接的方法居然接近最快......时间复杂度O(n* log_10{right})
优化
考虑预处理 + 索引,不过意义不是很大感觉
思考
- 先把最简单的做出来再说难的吧
747. 至少是其他数字两倍的最大数 ⭐

审题
- 最大整数的唯一性
- 至少是每个其他数字的两倍
- 能否在N的时间复杂度内完成?边找最大的边验证?
- 一种做法是先找到最大的数LogN 然后再遍历数组验证规则 LogN,时间复杂度是LogN
1. LogN的两次循环
审题时的想法,比较简单,两次LogN的搜索即可完成
public int dominantIndex(int[] nums) {
int max = nums[0];
int sum = 0;
int index = 0;
for(int i = 1; i < nums.length; i++) {
if(nums[i] >= max) {
max = nums[i];
index = i;
}
}
for(int i = 0; i < nums.length; i++) {
if(nums[i] == max)
continue;
if(nums[i] * 2 <= max)
sum++;
}
if(sum == nums.length - 1)
return index;
return -1;
}
2. 同时找到最大值和次大值
没深想,稍微想到了这里
找到次大值只要判断次大值是否大于最大值即可,即省去了之后的第二次LogN的判断操作,但从整体的时间复杂度来看两者是一样的
781. 森林中的兔子(华为) ⭐⭐
思考
注意回答是还有几只兔子颜色相同,注意相同数字的索引集合数目,是否超过其本身数字,肯定是需要遍历全的,至少On复杂度
1. 哈希表+计数清零
public int numRabbits(int[] answers) {
int total = 0;
if(answers.length == 0) {
return total;
}
HashMap<Integer,Integer> hashMap = new HashMap<>(answers.length);
int[] nums = new int[answers.length];
for(int i = 0; i < answers.length; i++) {
int sCount = answers[i];
hashMap.put(sCount,hashMap.getOrDefault(sCount,0)+1);
if(hashMap.get(sCount) > sCount + 1) {
total += sCount + 1;
hashMap.put(sCount,1);
}
}
for (Integer integer : hashMap.keySet()) {
total += integer + 1;
}
return total;
}
这里主要解决的问题就是在(1,1,1,1,1)的这种情况下,排除都是同一类的情况,在超过总和时,直接增加到最终计数中
2. 数组代替哈希表
public int numRabbits(int[] answers) {
int total = 0;
if(answers.length == 0) {
return total;
}
int max = 0;
for(int i = 0; i < answers.length; i++) {
if(max < answers[i])
max = answers[i];
}
int[] nums = new int[max+1];
for(int i = 0; i < answers.length; i++) {
int sCount = answers[i];
nums[sCount]++;
if(nums[sCount] > sCount + 1) {
total += sCount + 1;
nums[sCount] = 1;
}
}
for(int i = 0; i<=max; i++) {
if(nums[i] != 0) {
total += i + 1;
}
}
return total;
}
考虑到哈希表读取速度,以及后续扩容问题(但我这里提前设置容量,所以不存在)。为了节省时间,这里采用原来方法的数组代替哈希表的存取操作,先遍历一次,取得最大值。
后续这里的改进主要是可以从max 和min值,对nums容量进行空间范围的缩小。
3. 数学方法(不太懂)

public int numRabbits(int[] answers) {
Map<Integer, Integer> count = new HashMap<Integer, Integer>();
for (int y : answers) {
count.put(y, count.getOrDefault(y, 0) + 1);
}
int ans = 0;
for (Map.Entry<Integer, Integer> entry : count.entrySet()) {
int y = entry.getKey(), x = entry.getValue();
ans += (x + y) / (y + 1) * (y + 1);
}
return ans;
}
遗留问题
HashMap的四种遍历,哪种快一点?
819. 最常见的单词 ⭐
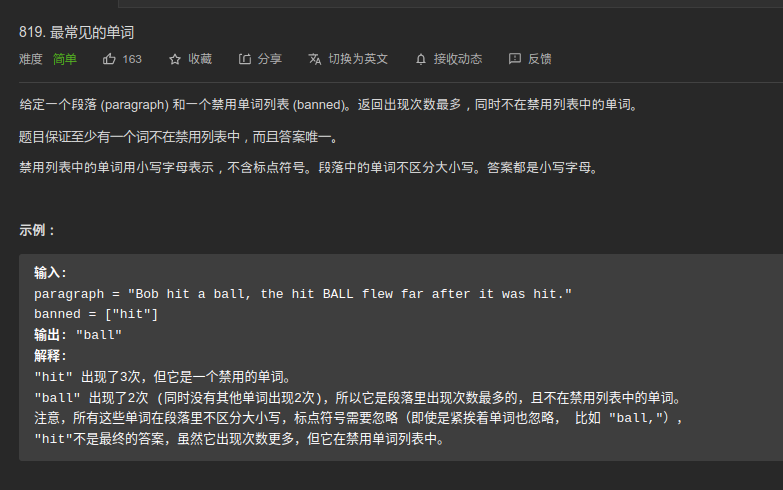
审题
- 要求:不在禁用列表中,且出现次数最多。
- 猜想:必须要遍历一次
1. Hash
读取每个单词,然后看Hash表中有无相同的元素(且不为-1,-1代表是被禁止的),然后实行自增,维护一个变量记录当前的最大出现次数的单词。优化点是没有用当前单词去循环比较banned数组看有没有被禁止的单词,而是用了哈希表的方式,比较快速。(代码写的很丑,严格意义上答案的题解不是一个段落,有例如"Bob"这样的字符串,没有以 . 结尾)
public String mostCommonWord(String paragraph, String[] banned) {
Map<String,Integer> strMap = new HashMap<>();
int begin = 0;
int start = 0;
int end = 0;
String curMax = "";
for(int i = 0; i < banned.length; i++) {
strMap.put(banned[i],-1);
}
for(int i = 0; i < paragraph.length(); i++) {
if(begin == 0 && (paragraph.charAt(i) >= 'a' && paragraph.charAt(i) <= 'z' || paragraph.charAt(i) >= 'A' && paragraph.charAt(i) <= 'Z' )) {
start = i;
begin = 1;
}else if(begin == 1 && (paragraph.charAt(i) >= 'a' && paragraph.charAt(i) <= 'z' || paragraph.charAt(i) >= 'A' && paragraph.charAt(i) <= 'Z' )&& i == paragraph.length() - 1){
end = i;
begin = 0;
String curWord = paragraph.substring(start,end + 1).toLowerCase();
int numInMap = strMap.getOrDefault(curWord,0);
if(numInMap != -1) {
strMap.put(curWord,numInMap+1);
curMax = strMap.getOrDefault(curMax,0) > numInMap + 1? curMax : curWord;
}
}else if(begin == 1 && ((paragraph.charAt(i) < 'a' || paragraph.charAt(i) > 'z') && ( paragraph.charAt(i) > 'Z'|| paragraph.charAt(i) < 'A'))) {
end = i;
begin = 0;
String curWord = paragraph.substring(start,end).toLowerCase();
int numInMap = strMap.getOrDefault(curWord,0);
if(numInMap != -1) {
strMap.put(curWord,numInMap+1);
curMax = strMap.getOrDefault(curMax,0) > numInMap + 1? curMax : curWord;
}
}
}
return curMax;
}
反思
- 题解中更好的方法去**判断当前字符是否是英文字符(包括大小写):Character.isLetter();**题解用Set去维护的banned数组,一样的思路,更加简洁
821. 字符的最短距离 ⭐
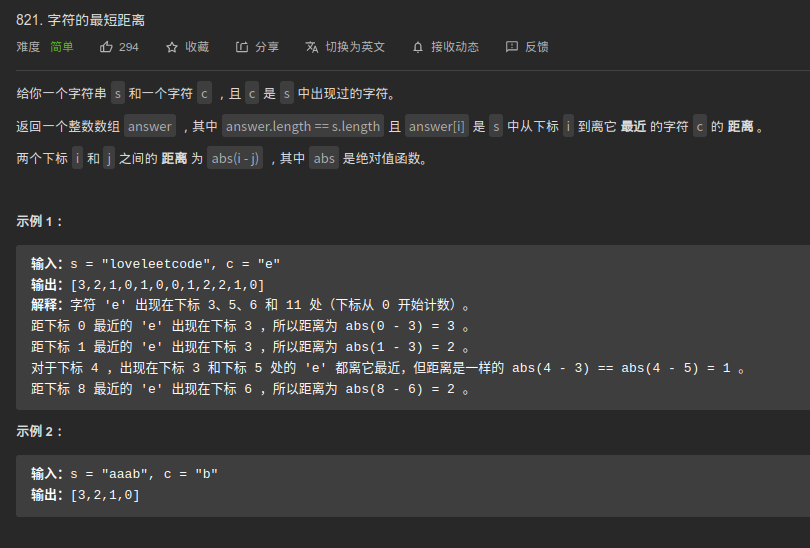
审题
- 返回的距离是最近的。
- 想法:双指针?
- 思路:
- 直接:
- 双指针:i用于作为外部循环,i != c时,则 j++,j负责找到最近的c,当i超过j时,维护旧的j,需要找新的c来做Math.min的判断
- 直接:
1. 双指针
区间问题,维护两个指针和一个变量,先找到第一个较近的相等字符索引位置 k
- 当前迭代序号 < 靠后指针索引且靠后指针有效(靠前指针指向的不是最后一个相等字符的索引):则需要比较与靠前和靠后指针索引的最小值
- 当前迭代序号 > 靠后指针索引且靠后指针有效:更新靠后指针与靠前指针(需要注意界限问题,与最开始靠前指针的取值条件)
- 靠后指针无效,则直接取值为:当前位置-靠前指针
public int[] shortestToChar(String s, char c) {
// i: 当前遍历的字符索引 j: 靠前的与c相等的字符索引 k: 靠后的与c相等的字符索引
int i,j = -1;
int k = -1;
int[] res = new int[s.length()];
while(s.charAt(++j) != c){}
for(i=0; i < s.length(); i++) {
if(k == -1 && i <= j) {
res[i] = Math.abs(i - j);
}else if(i <= j) {
if(s.charAt(j) == c) {
res[i] = Math.min(i - k, j - i);
}else{
res[i] = i - k;
}
}else if(i > j) {
k = j;
while(s.charAt(++j) != c && j < s.length() - 1){}
if(s.charAt(j) != c) {
res[i] = i - k;
}else{
res[i] = Math.min(i - k, j - i);
}
}
}
return res;
}
O(n+n)的时间复杂度
2. 集合
先遍历一次把所有的相同字符索引存起来,然后通过每次迭代时判断当前索引与集合中索引的关系即可,思路与上解相似。但时间复杂度很低,考虑可能需要先遍历一次字符串?
public int[] shortestToChar(String s, char c) {
int i,j = -1;
int[] res = new int[s.length()];
ArrayList<Integer> list = new ArrayList<>();
for(i = 0; i <s.length(); i++) {
if(s.charAt(i) == c){
list.add(i);
}
}
for(i = 0,j = 0; i <s.length(); i++) {
if(j == list.size()) {
res[i] = Math.abs(i - list.get(j-1));
}
else if(j == 0 && i <= list.get(j)){
res[i] = list.get(j) - i;
}else if( i > list.get(j)){
j++;
i--;
continue;
}else if(i <= list.get(j)){
res[i] = Math.min(list.get(j) - i, i - list.get(j - 1));
}
}
return res;
}
908. 最小差值I ⭐
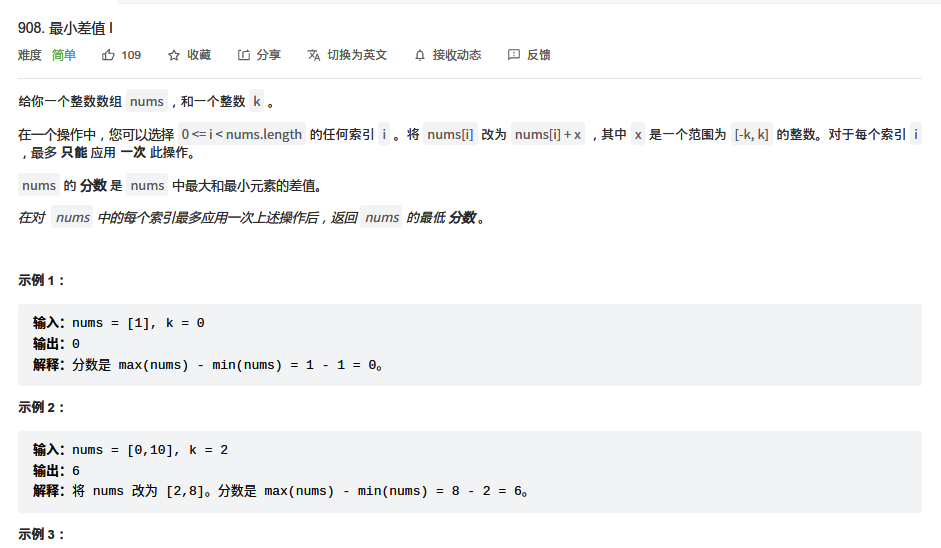
审题
- 核心:在对每个数在[-k,k]的变化范围内,是否与另一个数相减有最小值
- 分析:
- 每个数都必须遍历一次!最佳时间复杂度是On
- 思路:
- 直接:
- 先确定最小值最大值
- 如果差值小于2 * k,则直接等于0
- 若差值大于2 * k,则返回差值-2k的值?
- 先确定最小值最大值
- 直接:
1. 遍历
遍历找最大值,和最小值,与2 * k 的值进行比较。On的时间复杂度,O1的空间复杂度
public int smallestRangeI(int[] nums, int k) {
int min = nums[0];
int max = nums[0];
for(int num: nums) {
min = Math.min(num, min);
max = Math.max(num, max);
}
if(max - min <= 2 * k) {
return 0;
}else{
return max - min - 2 * k;
}
}

反思
- Math.max或者Math.min部分影响内存消耗和执行用时,直接换成三目运算符
954. 二倍数对数组 ⭐⭐
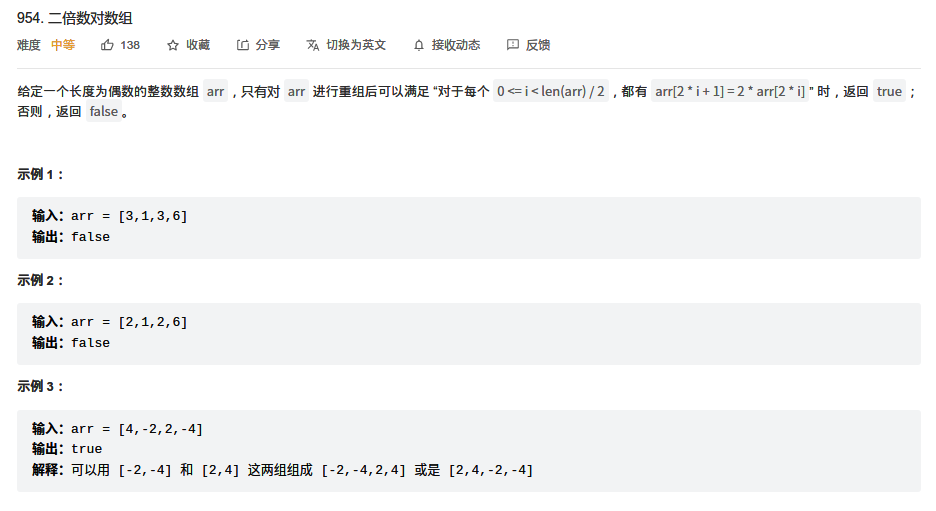
审题
- 长度为偶数,已给定.要对arr进行重组
- 可能的算法:
- 思路:
- 直接:
- 实际就每个数要有一个对应的数要么是它的二倍要么是它的2/1,考虑用哈希表,存储数据值和这个数出现的数目。再次遍历,查这个数的2倍或者2/1是否存在。(但可能的情况是,先找2倍,但后面会发现不满足[4,8,2,16],所以可能用到回溯)
- 直接:
1. 哈希+DFS(超时)
比较直接但很麻烦的想法,对原始数组,先遍历一次,计数放入哈希表中;针对递增索引,都进行情况为 num / 2 和 num*2的哈希查询,如果不为0,则两者计数都-1并进入下一层,DFS,回到本层时要还原现场。因为DFS,所以浪费了很多时间,没有必要,超时了理所当然
public boolean canReorderDoubled(int[] arr) {
Map<Integer, Integer> map = new HashMap<>();
for(int i = 0; i < arr.length; i++) {
int tmp= map.getOrDefault(arr[i],0);
map.put(arr[i],tmp + 1);
}
return dfs(map,0,arr,arr.length / 2);
}
public boolean dfs(Map<Integer, Integer> map,int i,int[] arr,int count) {
// 匹配成功
if(count == 0) {
return true;
}
// 这个数已经被用了
while(i < arr.length && map.get(arr[i]) == 0) {
i++;
}
if(i == arr.length) {
return false;
}
boolean a = false;
boolean b = false;
// 奇偶判断,如果是奇数,则num/2的情况肯定是false的(num为整数)
if(Math.abs(arr[i]) % 2 == 0) {
a = (map.getOrDefault(arr[i] / 2,0) > 0);
}
b = (map.getOrDefault(arr[i] * 2,0) > 0);
if(a) {
map.put(arr[i] / 2,map.get(arr[i] / 2) -1);
map.put(arr[i],map.get(arr[i]) -1);
a = dfs(map,i+1,arr,count - 1);
// 还原现场
map.put(arr[i] / 2,map.get(arr[i] / 2) + 1);
map.put(arr[i],map.get(arr[i] ) + 1);
}
if(b) {
map.put(arr[i] * 2,map.get(arr[i] * 2) -1);
map.put(arr[i],map.get(arr[i]) - 1);
b = dfs(map,i+1,arr,count - 1);
map.put(arr[i] * 2,map.get(arr[i] * 2) + 1);
map.put(arr[i],map.get(arr[i]) + 1);
}
return a | b;
}
2. 排序+迭代
加上了排序,这样就能避免在无序的数组中通过回溯的方式查找。通过有序的方式从小到大的搜索。并且有易忽略点:对于有序数组,对于负数,其实是arr[i*2] == arr[i * 2+1] * 2,而不能直接用题述的arr[2 * i + 1] == arr[i * 2](注意点)
这里其实还有一个数学原理:
对于有序排序的数组中的一个数,索引为i,如果满足上述题述条件,则必定在[ i, i + (arr.length / 2) ]的索引范围中找到这个数,所以这里我还可以做一个优化,将内循环由最多n次优化到n/2次,当然还是需要在数组的边界范围内,不过这个优化不是特别重要
public boolean canReorderDoubled(int[] arr) {
Arrays.sort(arr);
int zero_idx = arr.length;
for(int i =0; i < arr.length; i++) {
if(arr[i] > 0) {
if((i % 2) == 0) {
zero_idx = i;
break;
}else{
// 优化:如果零的个数为奇数,则肯定不匹配
return false;
}
}
}
// 设置标志位,判断这个索引上的数是否被用了
int[] flag = new int[arr.length];
int k = 0;
// 从非正整数位置开始
for(int i = zero_idx - 1 ; i >= 0; i--) {
k = i;
// 已被使用
if(flag[i] == 1)
continue;
while(k > 0){
if(arr[--k] == 2 * arr[i] && flag[k] == 0) {
flag[i] = 1;
flag[k] = 1;
break;
}
}
}
// 从正整数位置开始
for(int i = zero_idx ; i < arr.length - 1; i++) {
k = i;
if(flag[i] == 1)
continue;
while(k < arr.length - 1){
if(arr[++k] == 2 * arr[i] && flag[k] == 0) {
flag[i] = 1;
flag[k] = 1;
break;
}
}
}
// 可优化
for(int i = 0; i < arr.length; i++) {
if(flag[i] == 0)
return false;
}
return true;
}
因为内循环,所以达到了O(n *2)的时间复杂度
O(n)的空间复杂度
其实这里都浪费了很多时间,比如在对某一索引遍历时还可以判断,如果while结束后某一次flag[i] == 0,说明没有找到想要的值,可以直接返回false,稍加修改后这里用时提升到433ms,接近一半
3. 排序+哈希
很经典的提到了迭代搜索,那不然就有哈希表用空间换时间的操作,并且哈希表也在On的空间复杂度, 在时间复杂度上比flag数组更好。算是1和2的结合,但需要注意特殊情况,arr[i] = 0的时候 arr[i] * 2 也等于0
public boolean canReorderDoubled(int[] arr) {
Arrays.sort(arr);
int zero_idx = arr.length;
int count = 0;
Map<Integer,Integer> map = new HashMap<>();
for(int i =0; i < arr.length; i++) {
map.put(arr[i],map.getOrDefault(arr[i],0) +1);
if(zero_idx == arr.length && arr[i] > 0) {
if((i & 1) == 0) {
zero_idx = i;
}else{
return false;
}
}
}
for(int i = zero_idx - 1 ; i >= 0; i--) {
// 数已被使用
if(map.getOrDefault(arr[i],0) == 0){
continue;
}
if(map.getOrDefault(arr[i] * 2 ,0) > 0) {
if(arr[i] == 0) {
if(map.get(0) > 1) {
map.put(0, map.get(arr[i]) - 2);
count++;
}
}else{
map.put(arr[i] ,map.get(arr[i]) - 1);
map.put(arr[i] * 2,map.get(arr[i] * 2) -1);
count ++;
}
}
}
// 对arr[0] = 0 的情况的特殊判断,因为此时arr[i] * 2也等于0
for(int i = zero_idx ; i < arr.length - 1; i++) {
if(map.getOrDefault(arr[i],0) == 0){
continue;
}
if(map.getOrDefault(arr[i] * 2 ,0) > 0) {
if(arr[i] == 0 ) {
// 0存在的数目>2才能采用
if(map.get(0) > 1){
map.put(0,map.get(arr[i]) - 2);
count ++;
}
}else{
map.put(arr[i] ,map.get(arr[i]) - 1);
map.put(arr[i] * 2,map.get(arr[i] * 2) -1);
count ++;
}
}
}
if(count < arr.length /2) {
return false;
}
return true;
}
时间复杂度一下就快了很多了,因为消除了内层的循环,时间复杂度仅取决于Arrays.sort的排序复杂度
优化
特殊数:零,如果零的个数是奇数,则可以直接判false,并且也消除了之前对0的特殊判断
public boolean canReorderDoubled(int[] arr) {
Arrays.sort(arr);
int zero_idx = arr.length;
int count = 0;
int zero_count = 0 ;
Map<Integer,Integer> map = new HashMap<>();
for(int i =0; i < arr.length; i++) {
map.put(arr[i],map.getOrDefault(arr[i],0) +1);
if(arr[i] == 0) {
zero_count++;
}
if(zero_idx == arr.length && arr[i] > 0) {
if((i & 1) == 0) {
zero_idx = i;
}else{
return false;
}
}
}
// 0的个数是奇数,直接判false
if((zero_count & 1) == 1) {
return false;
}
// 从负数开始
for(int i = zero_idx - 1 - zero_count ; i >= 0; i--) {
if(map.getOrDefault(arr[i],0) == 0){
continue;
}
if(map.getOrDefault(arr[i] * 2 ,0) > 0) {
map.put(arr[i] ,map.get(arr[i]) - 1);
map.put(arr[i] * 2,map.get(arr[i] * 2) -1);
count ++;
}
}
// 从正数开始
for(int i = zero_idx ; i < arr.length - 1; i++) {
if(map.getOrDefault(arr[i],0) == 0){
continue;
}
if(map.getOrDefault(arr[i] * 2 ,0) > 0) {
map.put(arr[i] ,map.get(arr[i]) - 1);
map.put(arr[i] * 2,map.get(arr[i] * 2) -1);
count ++;
}
}
// 注意补上零的个数
if(count < (arr.length - zero_count) /2) {
return false;
}
return true;
}
有所提升,但是感觉不能再在这个算法上往上提升了,优化差不多就是这些了 ....
题解
官方解答思路差不多不过有大优化。都是排序数组中选择,并且也有我之前的优化步骤,这里因为排序有技巧:是通过绝对值大小排序的。统计Map中的数进入有序的集合中,然后根据集合中去判断所以可以不用再 map.put(x,map.get(x) - 1)
class Solution {
public boolean canReorderDoubled(int[] arr) {
Map<Integer, Integer> cnt = new HashMap<Integer, Integer>();
for (int x : arr) {
cnt.put(x, cnt.getOrDefault(x, 0) + 1);
}
if (cnt.getOrDefault(0, 0) % 2 != 0) {
return false;
}
List<Integer> vals = new ArrayList<Integer>();
for (int x : cnt.keySet()) {
vals.add(x);
}
// 好思路:根据绝对值顺序排序,就不用我这样判断情况了
Collections.sort(vals, (a, b) -> Math.abs(a) - Math.abs(b));
// 重点是从map的keySet中找,能一次就找完某个数在数组中所有分布的对应值
for (int x : vals) {
if (cnt.getOrDefault(2 * x, 0) < cnt.get(x)) { // 无法找到足够的 2x 与 x 配对
return false;
}
cnt.put(2 * x, cnt.getOrDefault(2 * x, 0) - cnt.get(x));
}
return true;
}
}
// 作者:LeetCode-Solution
// 链接:https://leetcode-cn.com/problems/array-of-doubled-pairs/solution/er-bei-shu-dui-shu-zu-by-leetcode-soluti-2mqj/
总结
- 🙅 被初始直接算法困扰。虽然做题原则上是从直接到进阶做,但是有时候直接的算法比较冗余,特殊情况较多,如果没写清楚,就容易混乱,导致恶性循环,也没心情想好的思路的。所以以后直接思路的实现比较繁琐时且知道效率不高时,要考虑去思考其他的方法了,不应该把重心放在冗余上。
- ⚠️ 排序数组在负数与正数在倍数关系上的相反情况!还有一些特殊情况的查找,以后读题时对关键条件要先找到特殊情况
- 👍 优化做的不错,能想到的优化点比较多。
- 迭代 向 哈希 的优化 多次经历了,记住
- 不太擅长的DFS磕磕绊绊做出来了,还行,不过还是磕磕绊绊....
- 愚人节快乐!
1221. 分割平衡字符串 ⭐
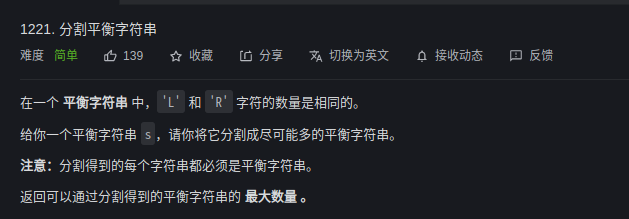
思考
每个字符串都是平衡字符串,这里父子存在相同关系,想到分治
列举不可能
长度为偶数、排除二分法、分支感觉无法完成
1. 叠加器迭代
想了一下,就是看两个字母在index处是否数目相同
public int balancedStringSplit(String s) {
int index = 0;
int r = 0;
int l = 0;
int count = 0;
while(index < s.length()) {
if(s.charAt(index) == 'L') {
l++;
}
else{
r++;
}
if(r == l) {
count++;
}
index++;
}
return count;
}
看了题解,可以只用一个符号位状态量记录L R的数值是否相等...稍微减少下内存占用
1282. 用户分组 ⭐⭐
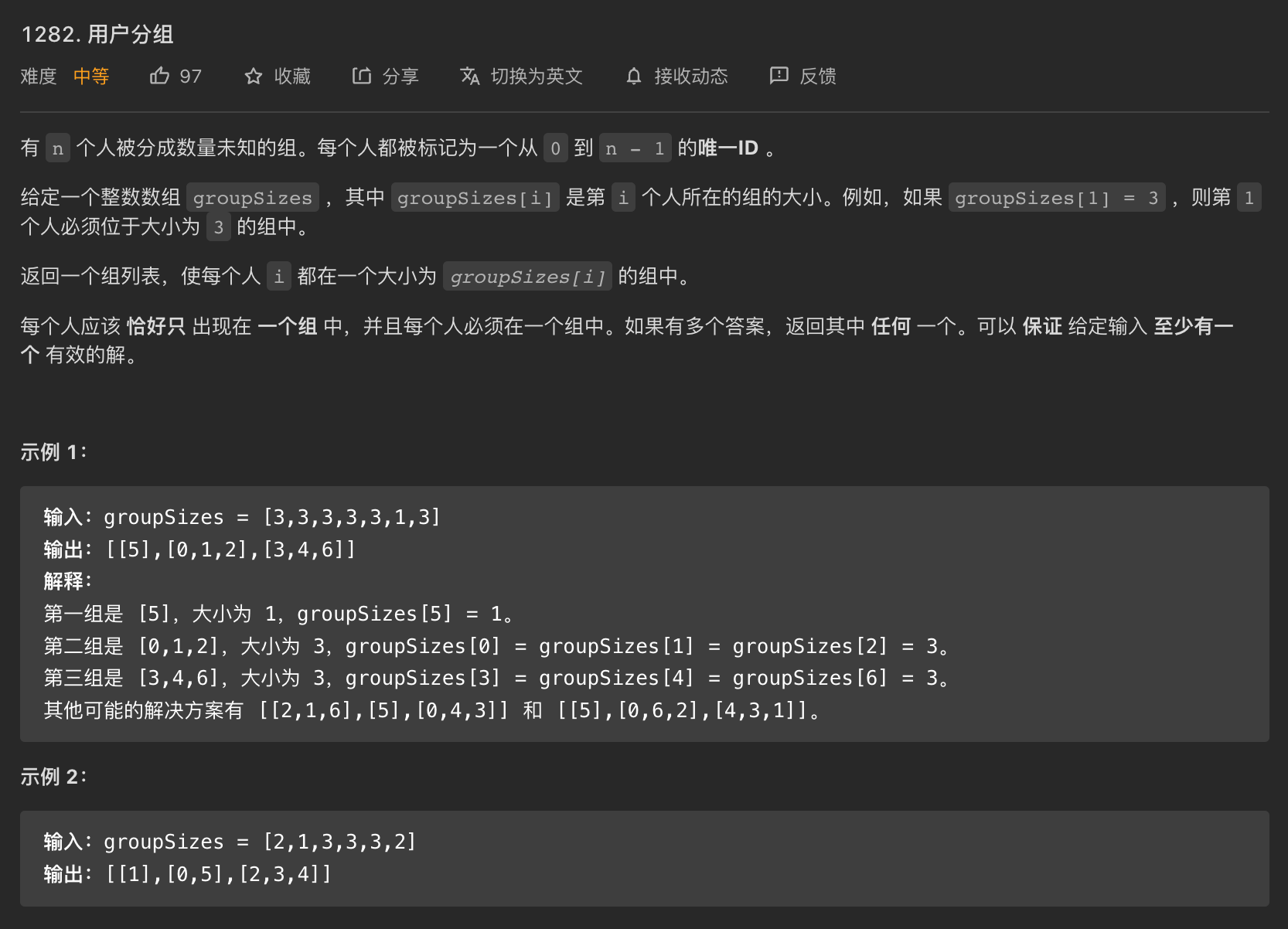
审题
- 可能的解法:
- 直接:把属于有n人组的那个人统计起来,然后随意分配
- 如何转化成数学问题?
- 组的人数必须说填充满的,而不能有余
- 难点:分组
- 能否在On的时间复杂度内做出来
1. Hash
思路还是比较清晰,将该分到n人组的那个人,分到n人组的第x组,如果第x组满了,那就再创建一个n人组把它放进去,否则则添加到x组的末尾即可,为了快速获取到n人组第x组是否人满的情况,建立一个n与n人组总人数的映射关系,但最终速度不理想...
class Solution {
public static List<List<Integer>> groupThePeople(int[] groupSizes) {
HashMap<Integer, List<List<Integer>>> groupListMap = new HashMap<>();
HashMap<Integer, Integer> groupNumMap = new HashMap<>();
for (int i = 0; i < groupSizes.length; i++) {
Integer groupNum;
if ((groupNum = groupNumMap.get(groupSizes[i])) == null) {
groupNumMap.put(groupSizes[i], 1);
List<List<Integer>> father = new ArrayList<>();
ArrayList<Integer> son = new ArrayList<>();
son.add(i);
father.add(son);
groupListMap.put(groupSizes[i], father);
} else {
List<List<Integer>> lists = groupListMap.get(groupSizes[i]);
if (groupNum % groupSizes[i] == 0) {
ArrayList<Integer> integers = new ArrayList<>();
integers.add(i);
lists.add(integers);
} else {
lists.get(groupNum / groupSizes[i]).add(i);
}
groupNumMap.put(groupSizes[i], ++groupNum);
}
}
List<List<Integer>> res = new ArrayList<>();
groupListMap.forEach((k, v) -> {
res.addAll(v);
});
return res;
}
}
简化
可进行如下简化,但时间优化不高,思想是一样的
class Solution {
public List<List<Integer>> groupThePeople(int[] gs) {
Map<Integer, List<Integer>> map = new HashMap<>();
for (int i = 0; i < gs.length; i++) {
List<Integer> list = map.getOrDefault(gs[i], new ArrayList<>());
list.add(i);
map.put(gs[i], list);
}
List<List<Integer>> ans = new ArrayList<>();
for (int k : map.keySet()) {
List<Integer> list = map.get(k), cur = new ArrayList<>();
for (int i = 0; i < list.size(); i++) {
cur.add(list.get(i));
if (cur.size() == k) {
ans.add(cur);
cur = new ArrayList<>();
}
}
}
return ans;
}
}
// 作者:AC_OIer
// 链接:https://leetcode.cn/problems/group-the-people-given-the-group-size-they-belong-to/solution/by-ac_oier-z1bg/
2. 内循环(N)
笑死,没想到内循环才是最快的。但确实,这里的精髓在于将已归纳的人“直接跳过”(通过置0+判断来实现),这样就能直接不使用HashMap来实现。猜测可能还是HashMap的一些方法,例如entrySet的遍历之类的会导致额外耗时
class Solution {
public List<List<Integer>> groupThePeople(int[] groupSizes) {
List<List<Integer>> result = new ArrayList<>();
for (int i = 0; i < groupSizes.length; i++) {
if (groupSizes[i] == 0) {
continue;
}
List<Integer> list = new ArrayList<>();
result.add(list);
list.add(i);
int size = groupSizes[i] - 1;
for (int j = i + 1; j < groupSizes.length && size > 0; j++) {
if (groupSizes[j] == groupSizes[i]) {
list.add(j);
groupSizes[j] = 0;
size--;
}
}
}
return result;
}
}
反思
这里内循环遍历(并通过设置特殊位跳过已经处理了的数据)是否近似实现了On的时间复杂度呢?我觉得是的🤔
1332. 删除回文序列 ⭐
审题
- 回文子序列 + 最少删除次数
- 如何找到回文子序列
1455. 检查单词是否位句中其他单词的前缀 ⭐
思考
- 输入是任何单词的前导连续子字符串
- 一次遍历
- 核心:抓住每一个单词,并且只用比较每一个单词与关键词相等长度的前缀是否相等即可(该单词长度必须大于等于关键词长度)
1. 一次遍历
先分割句子为单词字符串数组,然后筛选出长度大于等于关键词的单词,再去比较是否包含该单词,但要注意这里必须是从一开始就要包含。由于需要m个单词的字符串数组,所以空间复杂度较高(但由于测试用例问题,内存消耗还是有比较低的情况)
public int isPrefixOfWord(String sentence, String searchWord) {
String[] words = sentence.split(" ");
for(int i = 0; i < words.length; i++) {
if(words[i].length() >= searchWord.length()) {
if(words[i].substring(0, searchWord.length()).equals(searchWord)) {
return i + 1;
}
}
}
return -1;
}
优化-状态机
由于之前有Om的空间复杂度,所以要解决 不存储长度为m的字符串数组的问题,同时也要在一次遍历之内解决。这里便分情况来进行,有点状态机的思想。优点是在O(C)的空间复杂度和O(n)的时间复杂度内解决。但大量的if else结构还是让代码显得有点冗长
- 遇到空格:说明这个单词已经结束,应该重置一些变量
- 遇到空格后的第一个字符:查看字符与关键字是否相等
- 相等:新状态,开始比较下一个字符。如果这个过程中关键字比较完了,说明匹配成功,直接返回
- 不相等:新状态,该单词内所有字符都不用比较了
public int isPrefixOfWord(String sentence, String searchWord) {
// flag >= 0 searchword index in sentence
// flag == -1 not match
// flag == -2 this is a new word
int flag = -2;
int wordIdx = 1;
int sequence = 0;
for(int i = 0; i < sentence.length(); i++) {
if(sentence.charAt(i) == ' ') {
wordIdx++;
flag = -2;
sequence = 0;
}else if(flag == -2) { // flag == -2 this is a new word
if(sentence.charAt(i) == searchWord.charAt(sequence)) {
sequence++;
flag = -3;
}else{
flag = -4;
}
}else if(flag == -3){ // flag == -3 in matching
if(sentence.charAt(i) != searchWord.charAt(sequence)) {
flag = -4;
sequence = 0;
}else{
sequence++;
}
}else if(flag == -4) { // flag == -4 word matching fail(just for current word in sentence)
continue;
}
if(sequence >= searchWord.length()) {
return wordIdx;
}
}
return -1;
}

总结
状态机的思想:
- 能够在简化空间复杂度上有
- 能够帮助梳理思路,使逻辑结构清晰
1672. 最富有客户的资产总量 ⭐
Time : 2022 / 4 /14
TAG : Foreach
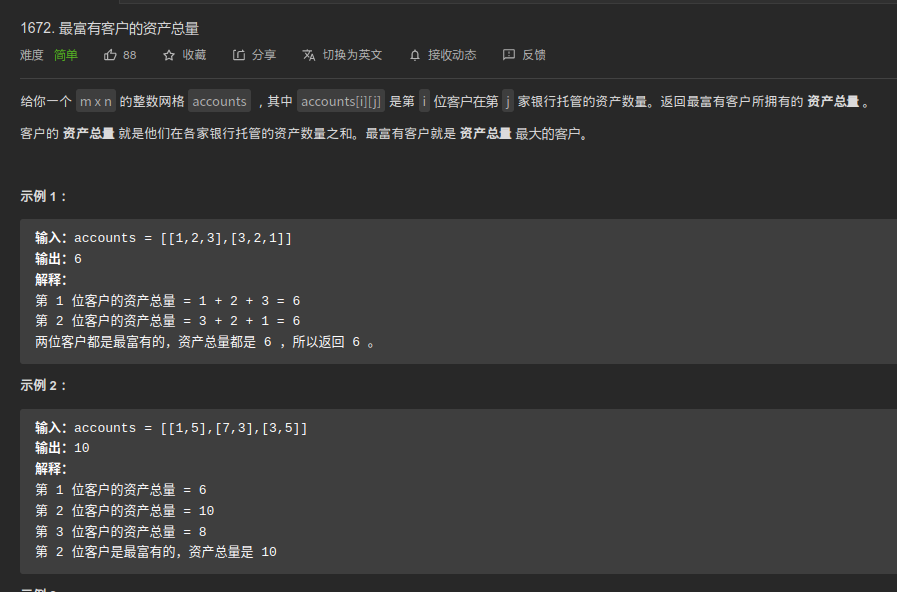
审题
- 就是返回一堆数组中最大数组值的数,肯定是O(i)*O(j)的遍历方式
public int maximumWealth(int[][] accounts) {
int max = 0;
for(int i = 0; i < accounts.length; i++) {
int temp = 0;
for(int j = 0; j <accounts[0].length; j++) {
temp += accounts[i][j];
}
max = Math.max(temp,max);
}
return max;
}
。。。。当我没有做过这道题
1716. 计算银行的钱 ⭐

审题
- 数学公式
- 变量累计
1. 暴力循环
public int totalMoney(int n) {
int sum = 0;
int div;
for(int i = 1; i <= n ; i++) {
div = (i-1) / 7;
if(i % 7 == 0) {
sum += div + 7;
}else{
sum += div + (i % 7);
}
}
return sum;
}
除法和求余操作耗时较多
2. 公式--等差数列
除了第一周外,剩下的每个整周比第一个周多出来的钱都是成等差数列的。省去LogN的逐步操作,先求出大部分,再求余下的
int sum = 0;
int left = n / 7 + 1;
int yu = n % 7;
if(left != 1){
sum += 28 * (left - 1) + ((left - 2)*(left - 1)) / 2 * 7;
// 注意这里求等差数列和
}
for(int i = 0 ; i < yu; i++) {
sum += left + i;
}
return sum;

加了个println结果耗时降到24%,蚌埠住了......
1894.找到需要补充粉笔的学生编号 ⭐⭐
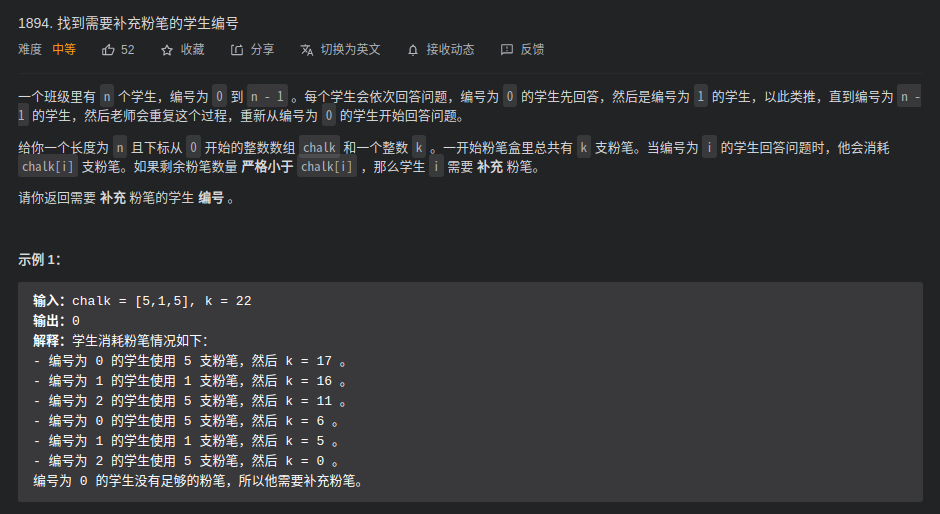
审题
输出的最后是需要补充粉笔的学生编号
1. 遍历模拟
public int chalkReplacer(int[] chalk, int k) {
int index = 0;
int singleTotal = 0;
int isRepeat = 0;
while(k-chalk[index] >= 0) {
if(isRepeat == 0) {
singleTotal += chalk[index];
}
if(isRepeat == 1 && index == 0) {
if(k - singleTotal >= 0) {
k-=singleTotal;
continue;
}
}
k-=chalk[index];
index++;
if(index >= chalk.length) {
index = 0;
isRepeat = 1;
}
}
return index;
}
这里原来直接遍历,但会超时,后面稍微改进了,使用一组的最大值稍作记录,但最终结果还是很慢,时间复杂度是O(n+m)
严格来说,遍历一次数组就应该知道是谁缺粉笔了
2. 优化
......通过先计算出Total,再模一组总数后进行查找就知道了。。。。这样看起来在一个循环里一样,但效率却快了很多很多,但两次循环,每次循环最多循环n次。时间复杂度是O(n),这里要注意一下:一样的思路不一样的处理方式,可能会在效率上造成很大差距
public int chalkReplacer(int[] chalk, int k) {
int index = 0;
long singleTotal = 0;
for(int i = 0; i<chalk.length; i ++) {
singleTotal += chalk[i];
}
k %= singleTotal;
while(k-chalk[index] >= 0) {
k-=chalk[index];
index++;
if(index >= chalk.length)
index = 0;
}
return index;
}
3. 前缀和+二分查找
(转)第一次找最大值,还是On
第二次去遍历时,这里在前缀和中找是哪一个使得singleTotal+=chalk[k]后大于了原来的k值,通过二分法找这里,复杂度为O(logn),但总的时间复杂度还是On。
public int chalkReplacer(int[] chalk, int k) {
int n = chalk.length;
if (chalk[0] > k) {
return 0;
}
for (int i = 1; i < n; ++i) {
chalk[i] += chalk[i - 1];
if (chalk[i] > k) {
return i;
}
}
k %= chalk[n - 1];
return binarySearch(chalk, k);
}
public int binarySearch(int[] arr, int target) {
int low = 0, high = arr.length - 1;
while (low < high) {
int mid = (high - low) / 2 + low;
if (arr[mid] <= target) {
low = mid + 1;
} else {
high = mid;
}
}
return low;
}
2024. 考试的最大困扰度 ⭐⭐
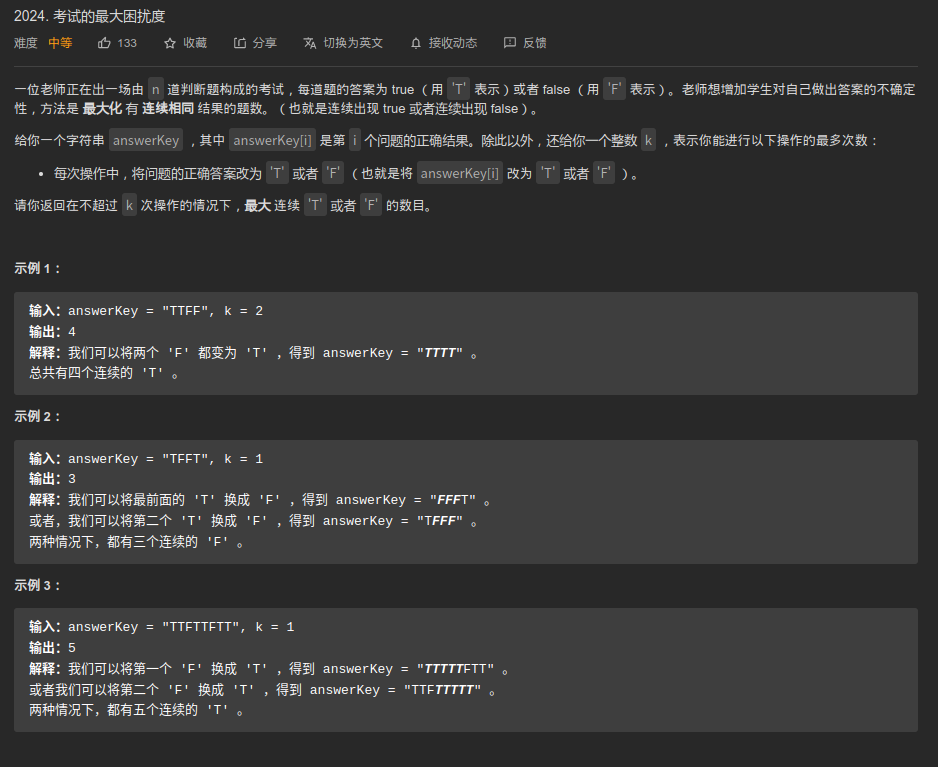
审题
- 目标:给定操作次数内把字符变为最大连续相同的个数
- 想法:要有最大连续相同,则k次操作改变的字符应该都是同一个
- 可能的做法:
- 思路
- 直接:找最大相同的子序列,和子序列与另一相同字符序列间隔的个数
- 进阶:
- 位运算
- 字符串->数组->一次遍历是否能够解决
1. 滑动窗口
没想到滑动窗口的思路,是看到题解提示才想到的,做的也很麻烦
与其我变不如它变,我维护一个最大能操作字符个数的区间,超过了我就移动到第一个操作区间的下一个字符,相当于改变区间起点
public int maxConsecutiveAnswers(String answerKey, int k) {
return Math.max(findMaxSequence(answerKey,k,1),findMaxSequence(answerKey,k,0));
}
int findMaxSequence(String s, int k, int mode) {
char a = (mode==1)?'F':'T';
char b = (mode==1)?'T':'F';
int count = 0;
int gap = 0;
int max = 0;
int start = 0;
for(int i = 0 ; i < s.length(); i++) {
if(s.charAt(i) == a){
if(gap < k){
gap++;
if(i == s.length() - 1) {
count = i - start + 1;
max = Math.max(count,max);
}
}else{
count = i - start ;
max = Math.max(count,max);
// 左移开始字符到第一个操作改变字符的下一个
while(start < s.length() - 1 && s.charAt(start++) == b);
if(i == s.length() - 1) {
count = i - start + 1;
max = Math.max(count,max);
}
}
}else{
if(i == s.length() - 1) {
count = i - start + 1;
max = Math.max(count,max);
}
}
}
return max;
}
缺点:过分考虑了i = s.length() - 1的情况
反向优化
队列缓存
初衷:操作次数大于限定值k时,要从第一个区间遍历去找第一个操作字符,这样有时间浪费。可以用一个队列将操作的字符的索引都缓存起来,然后直接去poll就行了。
public int maxConsecutiveAnswers(String answerKey, int k) {
return Math.max(findMaxSequence(answerKey,k,1),findMaxSequence(answerKey,k,0));
}
int findMaxSequence(String s, int k, int mode) {
int max = 0;
// b represent substitute
char b = (mode == 0?'F':'T');
Queue<Integer> list_s = new LinkedList<>();
list_s.offer(0);
for(int i = 0 ; i < s.length(); i++) {
if(s.charAt(i) == b){
if(list_s.size() <= k){
list_s.offer(i +1);
}else{
list_s.offer(i +1);
int a = list_s.size() == 0? 0 :list_s.poll();
max = Math.max(i - a ,max);
if(i == s.length() - 1)
break;
}
}
if(i == s.length() - 1) {
int a = list_s.size() == 0? 0 :list_s.peek();
max = Math.max(i - a + 1,max);
}
}
return max;
}
没懂为啥时间还慢一点,可能是队列的创建原因?
简洁(转)
LeetCode题解,与我第一个题解相似
public int maxConsecutiveChar(String answerKey, int k, char ch) {
int n = answerKey.length();
int ans = 0;
// 注意这种赋值,不错
for (int left = 0, right = 0, sum = 0; right < n; right++) {
// sum记录操作数
sum += answerKey.charAt(right) != ch ? 1 : 0;
// 移动起点到第一次操作的下一个位置
while (sum > k) {
sum -= answerKey.charAt(left++) != ch ? 1 : 0;
}
// 消除代码冗余
// 每次循环都比较一次,就不用做i=s.length() - 1的判断了
ans = Math.max(ans, right - left + 1);
}
return ans;
}
On时间复杂度 O1空间复杂度
一并计算(转)
这个思路 可以,精髓在于:没有具体要求到底是T 还是 F改变。我同时计算t操作和f操作的值,在同一始末点比较
- 如果不溢出,正常增长
- 如果只有其中一种操作数溢出,那表明另一种操作数没溢出,表明另一种操作数的总长>该种总长,可以继续运算。
- 如果两种都溢出,则表明都不行了,算最大值,并将l移动到两种都不溢出的情况
❓ 但这样就出现一个问题,为什么 L 移动的条件是两种都不溢出,而不是某一种不溢出?比如....FFFFFTTFT这样就要移动到T的位置再重新开始,但能否保证起点在前面的几个F中开始就一定没有最大值?- 没看题,条件是当两个均大于k才前进left,但只要有一个不满足就可以算了,是对的。在T满足情况时,F可能增加到远大于K,但没关系因为维护的是区间的缘故,之后都不满足时,遇到的F都会进行f-- 回退
class Solution {
public int maxConsecutiveAnswers(String answerKey, int k) {
// l:起始位置 r: 结束位置
int l = 0, r = 0;
int len = answerKey.length();
char[] cs = answerKey.toCharArray();
// t:改变T的操作次数 f:改变F的操作次数
int t = 0, f = 0;
int ans = 0;
while (r < len) {
char R = cs[r];
if (R == 'T') {
t++;
} else {
f++;
}
// 重点
if (t > k && f > k) {
ans = Math.max(ans, r - l);
while (t > k && f > k) {
char L = cs[l];
if (L == 'T') {
t--;
} else {
f--;
}
l++;
}
}
r++;
}
// 计算下最后的值
ans = Math.max(ans, len - l);
return ans;
}
}
// 作者:wa-pian-d
// 链接:https://leetcode-cn.com/problems/maximize-the-confusion-of-an-exam/solution/2024-kao-shi-de-zui-da-kun-rao-du-java-b-86wg/
总结
滑动窗口不熟悉,做的时候没有想到滑动窗口。好久没有做到滑动窗口的题了。滑动窗口题型的特点:有限定值,计算范围内的值(连续的),最好是在数组中进行的。巩固一下
对特殊情况的判断太多,造成思维混乱代码冗余
先想清楚再写代码…………
2034. 股票价格波动 ⭐⭐
审题
- 选取数据结构十分重要,max和min肯定是内部变量维护。
首先考虑数组 - update和最大最小的选取范围肯定是相关的,update最大最小值时从数组、链表角度都会引起On的时间复杂度
- update可以是未来的时间戳,所以数组可能不太现实
- 可能的做法:先考虑链表吧
1. 链表(超时)
class StockPrice {
Node head;
Node cur;
Node max;
Node min;
Node temp;
public StockPrice() {
}
public void update(int timestamp, int price) {
temp = new Node(price, timestamp, null);
if(head == null) {
head = temp;
cur = head;
max = head;
min = head;
}else{
if(max.val < temp.val) {
max = temp;
}
if(min.val > temp.val) {
min = temp;
}
if(cur.date < temp.date) {
cur.next = temp;
cur = temp;
}else{
Node pre_head = new Node(0,0,head);
Node ppre_head = new Node(0,0,pre_head);
int isResearch = -1;
while(pre_head.next.date < temp.date){
pre_head = pre_head.next;
}
if(pre_head.next.date == temp.date) {
if(pre_head.next.val == max.val && max.val > temp.val || pre_head.next.val == min.val && min.val < temp.val) {
isResearch = 1;
}
pre_head.next.val = temp.val;
}else{
temp.next = pre_head.next;
pre_head.next = temp;
}
head = ppre_head.next.next;
if(isResearch == 1) {
min = max = head;
pre_head = new Node(0,0,head);
while(pre_head.next != null) {
min = min.val > pre_head.next.val?pre_head.next:min;
max = max.val < pre_head.next.val?pre_head.next:max;
pre_head = pre_head.next;
}
}
}
}
}
public int current() {
return cur.val;
}
public int maximum() {
return max.val;
}
public int minimum() {
return min.val;
}
class Node{
int val;
int date;
Node next;
Node(int val, int date, Node next) {
this.val = val;
this.date = date;
this.next = next;
}
Node(){}
}
}
分析一下:max和min都在O1的复杂度内返回,每次update都有On的时间复杂度,看起来是不太好,但也必须遍历啊。这里说我超出时间限制是update操作。难道用HashMap?
2. 哈希表+有序集合(转)
哈希表用来存储对应stamp的price,有序集合来维护price的有序集合
class StockPrice {
int maxTimestamp;
HashMap<Integer, Integer> timePriceMap;
TreeMap<Integer, Integer> prices;
public StockPrice() {
maxTimestamp = 0;
timePriceMap = new HashMap<Integer, Integer>();
prices = new TreeMap<Integer, Integer>();
}
public void update(int timestamp, int price) {
maxTimestamp = Math.max(maxTimestamp, timestamp);
int prevPrice = timePriceMap.getOrDefault(timestamp, 0);
timePriceMap.put(timestamp, price);
if (prevPrice > 0) {
prices.put(prevPrice, prices.get(prevPrice) - 1);
if (prices.get(prevPrice) == 0) {
prices.remove(prevPrice);
}
}
prices.put(price, prices.getOrDefault(price, 0) + 1);
}
public int current() {
return timePriceMap.get(maxTimestamp);
}
public int maximum() {
return prices.lastKey();
}
public int minimum() {
return prices.firstKey();
}
}
初始化复杂度O1
更新操作、返回最大值和最小值的时间复杂度是OlogN
3. 哈希表+2个优先队列
哈希表还是来存stamp-price这里
妙在优先队列实现了延迟删除,判断了stamp对应的price是否是真实的
class StockPrice {
int maxTimestamp;
HashMap<Integer, Integer> timePriceMap;
PriorityQueue<int[]> pqMax;
PriorityQueue<int[]> pqMin;
public StockPrice() {
maxTimestamp = 0;
timePriceMap = new HashMap<Integer, Integer>();
pqMax = new PriorityQueue<int[]>((a, b) -> b[0] - a[0]);
pqMin = new PriorityQueue<int[]>((a, b) -> a[0] - b[0]);
}
public void update(int timestamp, int price) {
maxTimestamp = Math.max(maxTimestamp, timestamp);
timePriceMap.put(timestamp, price);
pqMax.offer(new int[]{price, timestamp});
pqMin.offer(new int[]{price, timestamp});
}
public int current() {
return timePriceMap.get(maxTimestamp);
}
public int maximum() {
while (true) {
int[] priceTime = pqMax.peek();
int price = priceTime[0], timestamp = priceTime[1];
if (timePriceMap.get(timestamp) == price) {
return price;
}
pqMax.poll();
}
}
public int minimum() {
while (true) {
int[] priceTime = pqMin.peek();
int price = priceTime[0], timestamp = priceTime[1];
if (timePriceMap.get(timestamp) == price) {
return price;
}
pqMin.poll();
}
}
}
总结
- TreeMap不熟悉,根本没考虑,有空再了解一下TreeMap。HashMap看不上,觉得没有链表快.....
- 以后还是要多想一下,毕竟链表在插入时还是On的复杂度,但HashMap基本是O1,还是没有想清楚,所以会造成超时的问题。
2044. 统计按位或能得到最大值的子集数目 ⭐⭐
Time : 2022 / 3 /15 20 : 20
TAG:DFS、Bit
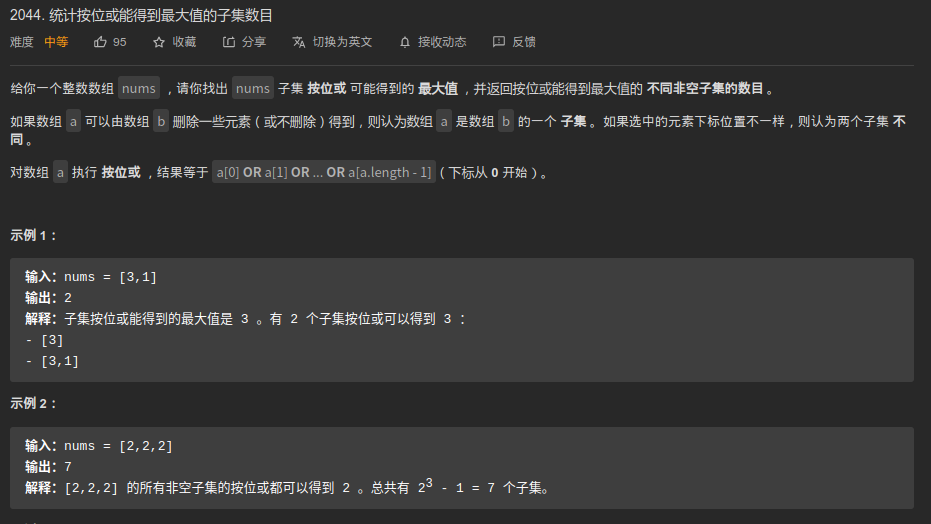
审题
- 最大值数目可能不唯一,求数目
- 细节:数组可能有相同元素,无排序顺序
- 难点:子集的 数目多,如何划分最大值子集。可能涉及DFS?
- 理论基础:
- 一个数可以变换成 c = a | b 的形式,则可以实现替代 。只要位数、
- 思路:首先最大值肯定是包含所有元素的值(题目给出的num[i] > 0),以此为基础
- 最暴力:求出所有子集的与,放在哈希表中,然后找结果
- 简单:先计算出最大值(全集),使用DFS依次去掉
- 进阶:
1. 位运算 (转)
一个已经忽略已久的应用: 位运算中一个数可看成是一个数组,1 代表选中 0 代表未选中
这里就用一个数来代表数组,目的是方便进行位数的左右移动 和 与或运算。外层代表的是是否选中n位数,总共有2 ^ nums.length ,内层则对其进行多次与运算
class Solution {
public int countMaxOrSubsets(int[] nums) {
int maxOr = 0, cnt = 0;
for (int i = 0; i < 1 << nums.length; i++) {
int orVal = 0;
for (int j = 0; j < nums.length; j++) {
if (((i >> j) & 1) == 1) {
orVal |= nums[j];
}
}
if (orVal > maxOr) {
maxOr = orVal;
cnt = 1;
} else if (orVal == maxOr) {
cnt++;
}
}
return cnt;
}
}
// 作者:LeetCode-Solution
// 链接:https://leetcode-cn.com/problems/count-number-of-maximum-bitwise-or-subsets/solution/tong-ji-an-wei-huo-neng-de-dao-zui-da-zh-r6zd/
时间复杂度:O(1 << nums.length) * O(nums.length)
空间复杂度:O(1)
2. 回溯 / DFS (转)
用的很巧妙,每次方法结束前回溯 主要是进行了不或的结果,实现了某一位数不参与运算的操作。这里的思路要好好学习
class Solution {
int[] nums;
int maxOr, cnt;
public int countMaxOrSubsets(int[] nums) {
this.nums = nums;
this.maxOr = 0;
this.cnt = 0;
dfs(0, 0);
return cnt;
}
public void dfs(int pos, int orVal) {
if (pos == nums.length) {
if (orVal > maxOr) {
maxOr = orVal;
cnt = 1;
} else if (orVal == maxOr) {
cnt++;
}
return;
}
dfs(pos + 1, orVal | nums[pos]);
dfs(pos + 1, orVal);
}
} }
// 作者:tong-zhu
// 链接:https://leetcode-cn.com/problems/count-number-of-maximum-bitwise-or-subsets/solution/by-tong-zhu-mmeu/
时间复杂度:O(1 << nums.length)
空间复杂度:O(nums.length) (调用栈占用空间)
优化
因为是顺序搜索的,或的结果是依次增大,所以先遍历一次求出max,如果在的dfs时其值等于max,则可以直接计算出结果
if (or == max) {
ans += 1 << (nums.length - i);
return;
}
再优化
前面步骤中是按顺序从0 开始 两种情况,算当前值和不算当前值 进行dfs的,还可以从广度上来看,对某一层来说,广度遍历其剩下元素或结果,如果等于max,则直接return
private void dfs(int[] nums, int i, int or, int max) {
if (or == max) {
ans += 1 << (nums.length - i);
return;
}
for (int j = i; j < nums.length; j++) {
dfs(nums, j + 1, or | nums[j], max);
}
}
尽管时间空间复杂度还是不变,但它优化了多数情况。只能说太强......
反思
- 太菜了太菜了,思路是在DFS上的 遍历得到max的思路也是有的,但纠结点在于 如何算一个集合的子集的或结果,嵌套循环都是不可能实现的,但DFS还是纠结于层数和索引,回溯思路不对
- 位运算 1 << nums.length 意义想清楚,位运算不仅仅只是与或的运算,还包含 1 0 表示的意义
2055. 蜡烛之间的盘子 ⭐⭐
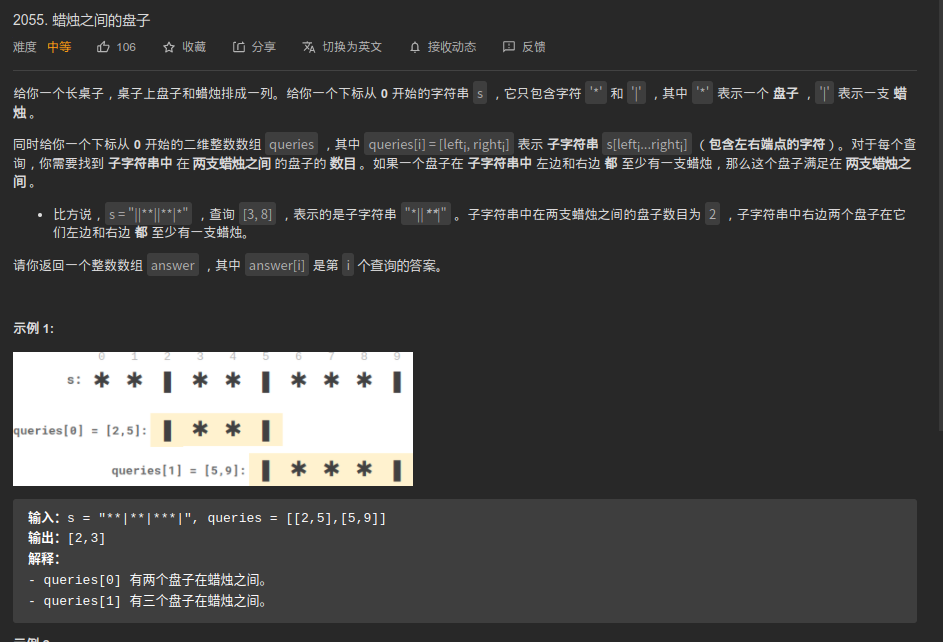
审题
- 第一眼:括号匹配-----> 栈(错了!)
- 查询索引的给出是乱序的
- 思路:
- 简单:把最近的 | 找到,然后找下一个 | ,中间的 * 则累加
- 进阶:
- 简单方法会重复遍历之前算过的部分序列,不方便。这里盲猜是线段树了,因为具体某段距离对结果有影响
- 恒久不变的话题:能不能一次遍历得到。即理想结果:我先遍历一次数组,然后你给我一个查询序列,我在O(C)的时间复杂度内返回每个结果(这个想法不错!)
1. 暴力双循环(X)
public int[] platesBetweenCandles(String s, int[][] queries) {
int[] res = new int[queries.length];
for(int i = 0; i < queries.length; i++) {
int num = 0;
int flag = 0;
int temp = 0;
for(int k = queries[i][0]; k < queries[i][1] +1; k++) {
if(flag == 0 && s.charAt(k) == '|') {
flag = 1;
}else if(flag == 1 && s.charAt(k) == '*') {
temp++;
}else if(flag == 1 && s.charAt(k) == '|') {
num += temp;
temp = 0;
}
}
res[i] = num;
}
return res;
}
超时,因为复杂度到O(n^2)了
2. 缓存索引(X)
把带 | 的索引位置都缓存下来,然后根据顺序找到最小的左开端,就能算出个数
class Solution {
public int[] platesBetweenCandles(String s, int[][] queries) {
int[] res = new int[queries.length];
List<Integer> candleIdx = new ArrayList<>();
for(int i = 0;i < s.length(); i++) {
if(s.charAt(i) == '|') {
candleIdx.add(i);
}
}
for(int i = 0; i < queries.length; i++) {
int leftIndex = -1;
int rightIndex = -1;
int candleCnt = 0;
for(int k = 0; k < candleIdx.size(); k++) {
if(leftIndex == -1 && candleIdx.get(k) >= queries[i][0] && candleIdx.get(k) <= queries[i][1]) {
leftIndex = k;
}else if(leftIndex != -1 && candleIdx.get(k) <= queries[i][1]) {
rightIndex = k;
}else if(candleIdx.get(k) > queries[i][1]) {
break;
}
}
if(leftIndex != -1 && rightIndex != -1) {
for(int k = leftIndex; k < rightIndex; k++) {
candleCnt += candleIdx.get(k+1) - candleIdx.get(k) - 1;
}
}else{
candleCnt = 0;
}
res[i] = candleCnt;
}
return res;
}
}
超时,O(n^2)时间复杂度。能不能不找 左临界值?
3. 缓存临界最值(X)
预处理的影子
方法2的改良版,通过哈希表缓存了每个索引下的之前最近的那个一个 | 的索引值,就不用在通过On的时间复杂度查找左临界值了,但还是超时
class Solution {
public int[] platesBetweenCandles(String s, int[][] queries) {
int[] res = new int[queries.length];
List<Integer> candleIdx = new ArrayList<>();
int[] mapInt = new int[s.length()];
int num = 0;
for(int i = 0;i < s.length(); i++) {
if(s.charAt(i) == '|') {
candleIdx.add(i);
}
mapInt[i] = candleIdx.size() - 1;
}
for(int i = 0; i < queries.length; i++) {
int leftIndex = mapInt[queries[i][0]] + 1;
int rightIndex = mapInt[queries[i][1]];
int candleCnt = 0;
if(s.charAt(queries[i][0]) == '|') {
leftIndex--;
}
if(leftIndex < rightIndex ) {
for(int k = leftIndex; k < rightIndex; k++) {
candleCnt += candleIdx.get(k+1) - candleIdx.get(k) - 1;
}
}else{
candleCnt = 0;
}
res[i] = candleCnt;
}
return res;
}
}
然而!!!!!!
在稍微看了下答案后,发现自己的思路和答案的前缀和有类似之处,发现自己的思路肯定也是可行的,就继续更改,前面的处理都没问题,主要是后面算累计和的时候,又进行了一次for循环,虽然很短,但从性能上来说,也不好,这也是造成超时的重要原因,就优化了一下:
if(leftIndex < rightIndex ) {
candleCnt += candleIdx.get(rightIndex) - candleIdx.get(leftIndex) - rightIndex + leftIndex; }
还是功夫不负有心人哈哈哈,这道题纠结了半天,最后还是回到正确思路上了
4. 预处理+前缀和(转)
答案的思路:
- 三个数组
- 记录 前n个数中 * 的总和
- 记录 第n个数中上一个 | 的索引
- 记录第n个数中 下一个 | 的索引
- 比较条件,二者不为-1 且左边 | 索引大于右边 | 索引,则结果就为最右临界值- 最左临界值(数值)【确实!】
class Solution {
public int[] platesBetweenCandles(String s, int[][] queries) {
int n = s.length();
int[] preSum = new int[n];
for (int i = 0, sum = 0; i < n; i++) {
if (s.charAt(i) == '*') {
sum++;
}
preSum[i] = sum;
}
int[] left = new int[n];
for (int i = 0, l = -1; i < n; i++) {
if ( s.charAt(i) == '|') {
l = i;
}
left[i] = l;
}
int[] right = new int[n];
for (int i = n - 1, r = -1; i >= 0; i--) {
if (s.charAt(i) == '|') {
r = i;
}
right[i] = r;
}
int[] ans = new int[queries.length];
for (int i = 0; i < queries.length; i++) {
int[] query = queries[i];
int x = right[query[0]], y = left[query[1]];
ans[i] = x == -1 || y == -1 || x >= y ? 0 : preSum[y] - preSum[x];
}
return ans;
}
}
// 作者:LeetCode-Solution
// 链接:https://leetcode-cn.com/problems/plates-between-candles/solution/zha-zhu-zhi-jian-de-pan-zi-by-leetcode-s-ejst/
这里拿空间换时间(3个N长度数组),所以空间复杂度低,但时间复杂度就高起来了,O(n+q) :On的时间预处理 O(q)处理q个询问(每个询问处理时间为O(1))
反思
- 简单算法上没浪费太多时间,还行
- 能想到缓存(即预处理) 进而想到一点点前缀和的思想,还可以
- 思路上能想到一次遍历,有预处理的影子,可以
- 前缀和不熟悉,预处理的想法还没建立在脑海中,慢慢发现不是线段树不是这种类型?前缀和这里的叠加思想做的时候没有想出来 即
若有值 值 = 最右不超出的索引值(origin) - 最左不超出的索引值(origin)
2100. 适合打劫银行的日子 ⭐⭐
2022 / 3 / 6 18:35
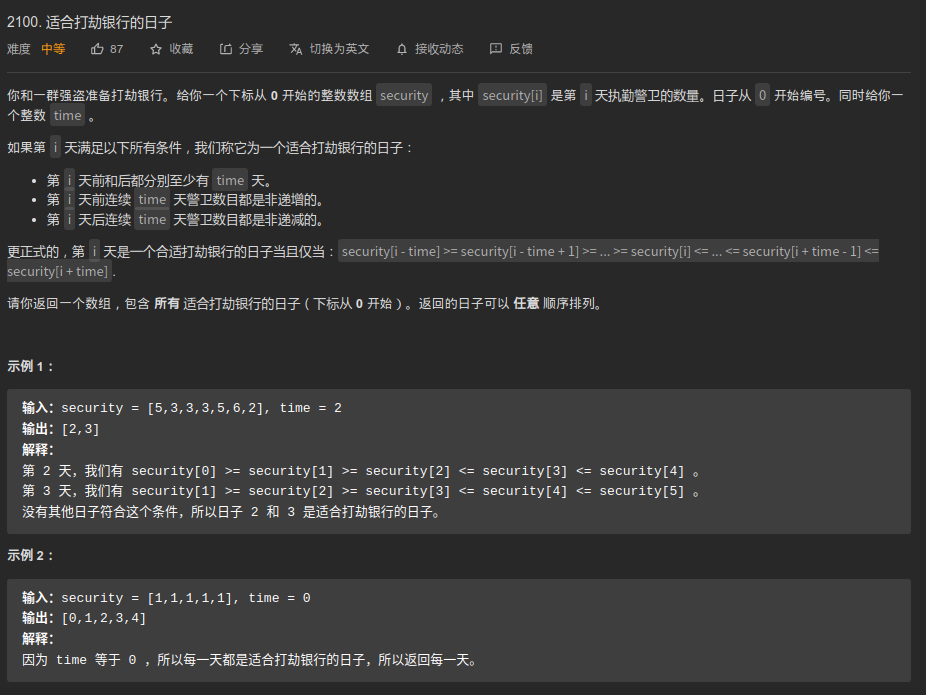
审题
- 下标从0开始,有第0天
- 返回的是所有可能的天数
- 问题核心:找到数组中给定间隔数中前段单减后段单增的数
- 可能的数据结构:滑动窗口?栈或队列?
- 思路:
- 基本:顺序判断
- 进阶:队列抽
1. 顺序遍历
思路还是依次遍历 + flag条件筛选,但这里为了解决题中的大量重复数组带来的超时限制,我就稍微优化了一下,增加了个前置条件的判断:如果上一个天数也是Rob Day,那只需要判断一下就可以知道这一天是不是Rob Day了,但实际上是没有解决时间复杂度的问题的。
class Solution {
public List<Integer> goodDaysToRobBank(int[] security, int time) {
List<Integer> res = new ArrayList<>();
if(2 * time >= security.length)
return res;
for(int i = time; i < security.length - time; i++) {
if(res.size() > 0 && res.get(res.size() - 1) == i - 1) {
if(security[i - 1] >= security[i] && security[i + time - 1] <= security[i + time] ){
res.add(i);
continue;
}
}
int flag = 0;
for(int k = 1; k <= time; k++) {
if(security[i - k + 1] > security[i - k]) {
flag = -1;
break;
}
}
if(flag == -1)
continue;
for(int k = 1; k <= time; k++) {
if(security[i + k - 1] > security[i + k]) {
flag = -1;
break;
}
}
if(flag == 0) {
res.add(i);
}
}
return res;
}
}
这个结果也是意料之中了,似乎暴力都是5%?不过内存消耗还不错
空间复杂度:O(n)
时间复杂度:
2. 滑动窗口(队列实现)
队列实现的滑动窗口,过期自动删除。未过期又在违规队列中,那就说明这个数不是合适的Rob Day
public List<Integer> goodDaysToRobBank(int[] security, int time) {
List<Integer> res = new ArrayList<>();
if(2 * time >= security.length)
return res;
// 避免零步长导致i-1 < 0 的情况
if(time == 0) {
for(int i = 0; i < security.length ; i++) {
res.add(i);
}
return res;
}
Queue<Integer> leftQueue = new LinkedList<>();
Queue<Integer> rightQueue = new LinkedList<>();
for(int i = 0; i < time; i++) {
if(security[i] < security[i + 1]){
leftQueue.offer(i);
}
if(security[time + i] > security[time + i + 1]) {
rightQueue.offer(i + time);
}
}
for(int i = time; time + i < security.length; i++) {
int flag = 1;
if(security[i - 1] < security[i]) {
leftQueue.offer(i-1);
}else if(security[i + time - 1] > security[time + i]) {
rightQueue.offer(i + time - 1);
}
while(!leftQueue.isEmpty()) {
int leftTemp = leftQueue.peek();
if(leftTemp < i - time){
leftQueue.poll();
}else{
flag = -1;
break;
}
}
while(!rightQueue.isEmpty()) {
int rightTemp = rightQueue.peek();
if(rightTemp < i){
rightQueue.poll();
}else{
flag = -1;
break;
}
}
if(flag == -1){
continue;
}
if(leftQueue.isEmpty() && rightQueue.isEmpty()) {
if( security[i - 1] >= security[i] && security[i + time - 1] <= security[time + i]) {
res.add(i);
}
continue;
}
}
return res;
}
真的不懂为啥这么慢啊,我感觉还行啊,也是在一次遍历就解决问题啊。。。
空间复杂度:On
时间复杂度:On (感觉)
3. 动态规划
我是傻逼之没想起dp........
class Solution {
public List<Integer> goodDaysToRobBank(int[] security, int time) {
int n = security.length;
int[] left = new int[n];
int[] right = new int[n];
for (int i = 1; i < n; i++) {
if (security[i] <= security[i - 1]) {
left[i] = left[i - 1] + 1;
}
if (security[n - i - 1] <= security[n - i]) {
right[n - i - 1] = right[n - i] + 1;
}
}
List<Integer> ans = new ArrayList<>();
for (int i = time; i < n - time; i++) {
if (left[i] >= time && right[i] >= time) {
ans.add(i);
}
}
return ans;
}
}
// 作者:LeetCode-Solution
// 链接:https://leetcode-cn.com/problems/find-good-days-to-rob-the-bank/solution/gua-he-da-jie-yin-xing-de-ri-zi-by-leetc-z6r1/
4. 双向遍历+哈希(转)
正向标记出前 time 天符合条件的日期,逆向遍历选出前后都符合的加入答案,还不是很理解。不过确实牛逼,双百趋向。
class Solution {
public:
vector<int> goodDaysToRobBank(vector<int>& security, int time) {
vector<int> ans;
int rear = -1, n = security.size(), cnt = 1;
for(int i = 0; i < n; ++i){
int x = security[i];
rear >= x ? ++cnt : cnt = 1;
if(cnt > time) security[i] ^= (1<<30);
rear = x;
}
rear = -1, cnt = 0;
for(int i = n-1; i >= 0; --i){
int x = security[i] &~ (1<<30);
rear >= x ? ++cnt : cnt = 1;
if(cnt > time && (security[i] >> 30)) ans.push_back(i);
rear = x;
}
return ans;
}
};
// 链接:https://leetcode-cn.com/problems/find-good-days-to-rob-the-bank/solution/gua-he-da-jie-yin-xing-de-ri-zi-by-leetc-z6r1/1418616
总结
- Queue还不是很熟悉
- 没想到dp.....偏偏这次没想到
- 其他还好,除了没想到好方法 还彳亍
------------------------------------------
LRU实现
阿里2020. 栈求表达式

计算整数n的平方根 精度为0.00001
牛顿迭代法
牛顿迭代法不安全
我的代码:
public static double sqrtByMyOwn(int num){
if(num==0)
return 0;
double result1,result2=Integer.MAX_VALUE;
double i=0;
while(i*i<num){
i+=0.5;
}
result1=i;
while(true){
result2=result1/2+num/(2*result1);
if(result1-result2<0.00001) {
BigDecimal b=new BigDecimal(result2);
double result=b.setScale(5, BigDecimal.ROUND_HALF_UP).doubleValue();
return result;
}
result1=result2;
}
}
本博客题解均转载于力扣官网 https://leetcode-cn.com,用于个人学习算法。如有侵权,请联系!